圆锥曲线
Date:
圓錐曲線(英語:conic section),又稱圓錐截痕、圓錐截面、二次平面曲線, 是數學、幾何學中通過平切圓錐(嚴格為一個正圓錐面和一個平面完整相切)得到 的曲線,包括圓,橢圓,拋物線,雙曲線及一些退化類型。
圓錐曲線在約公元前200年時就已被命名和研究了,其發現者為古希臘的數學家阿波羅尼奧斯(Apollonius), 那時阿波羅尼阿斯對它們的性質已做了系統性的研究。
圓錐曲線應用最廣泛的定義為(橢圓,拋物線,雙曲線的統一定義):動點到一定點(焦點) 的距離與其到一定直線(準線)的距離之比為常數(離心率$\displaystyle e$)的點的集合是 圓錐曲線。對於$\displaystyle 0<e<1$得到橢圓,對於$\displaystyle e=1$得到拋物線, 對於$\displaystyle e>1$得到雙曲線。
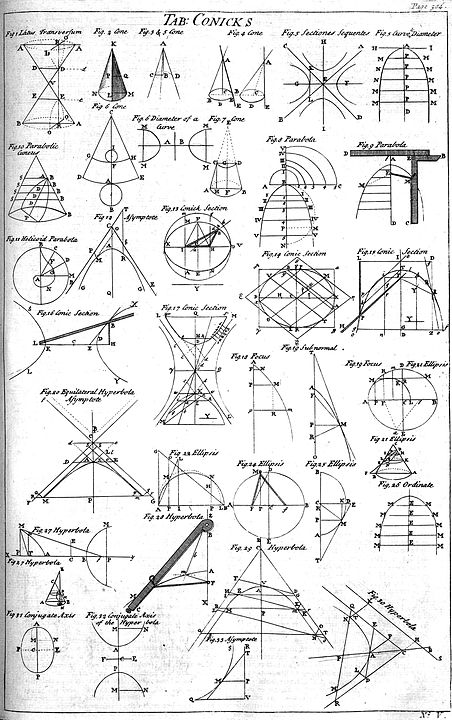
圓錐曲線的定義
作為圓錐面和平面的交線
如上圖所示,有三種圓錐曲線:橢圓(ellipse)、拋物線(parabola)和雙曲線(hyperbola)。圓作為橢圓 的一種特殊形式可以看作橢圓。
橢圓線:當平面切割圓錐面為一個閉合曲線時,該曲線為一個橢圓或者圓周;
拋物線:當切割平面與圓錐面的母線平行時截得到的曲線;
雙曲線:其它情形,相交曲線為雙曲線。
平面幾何定義
圓錐曲線在平面幾何中可以用到定點(焦點,focus)的距離等於常數倍的到定直線(對稱軸, directrix)的距離的所有點的軌跡。 這個常數定義為離心率(eccentricity $e$)。
當$0<e<1$時為橢圓;
當$e=1$ 時為拋物線;
當$e>1$時為雙曲線。
圓錐曲線在直角坐標下的標準方程
- 橢圓:$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$
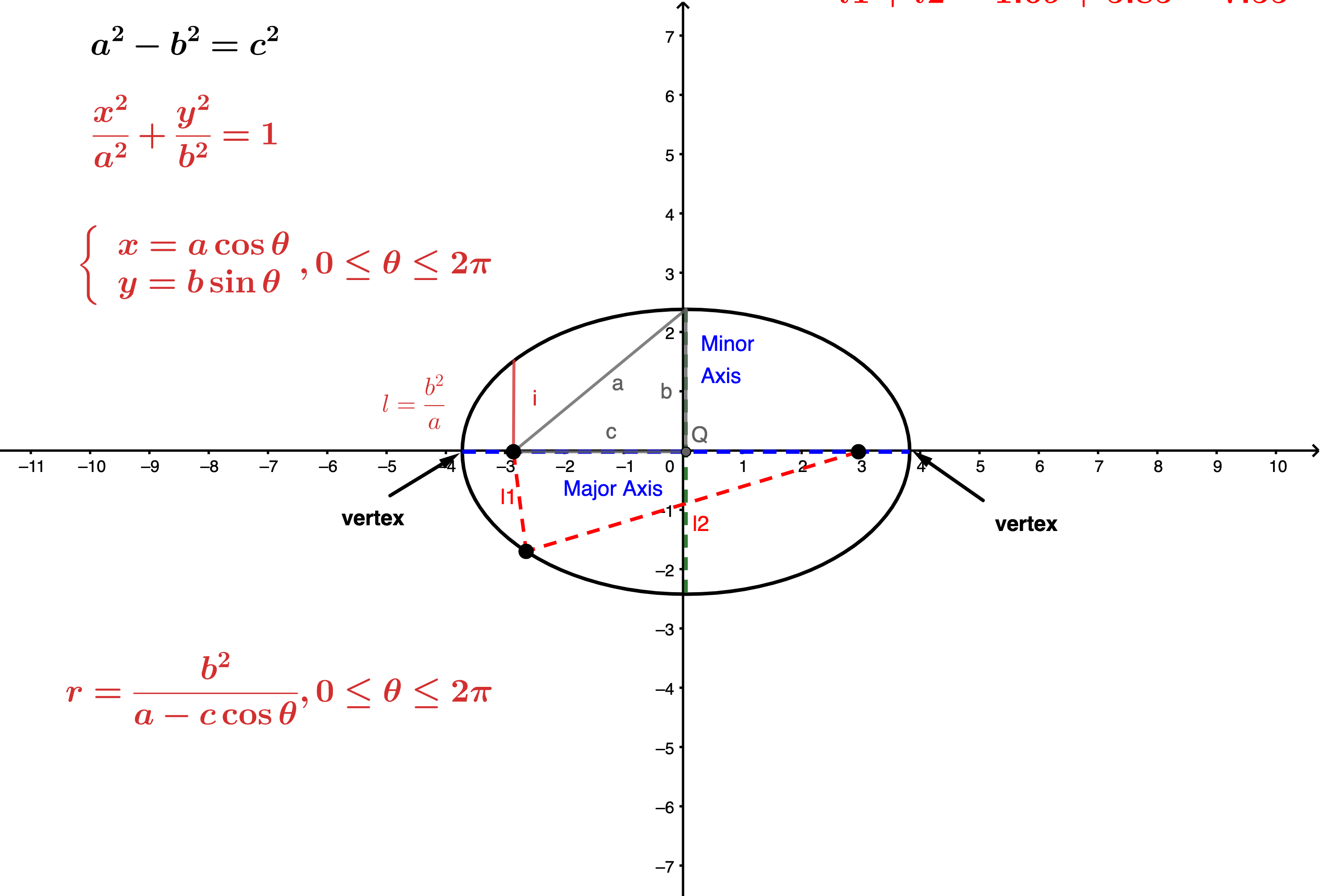
- 雙曲線:$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$
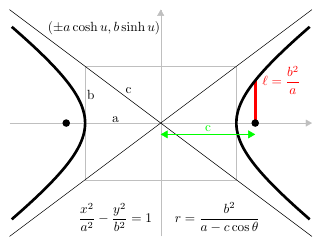
- 拋物線:$y=4ax$
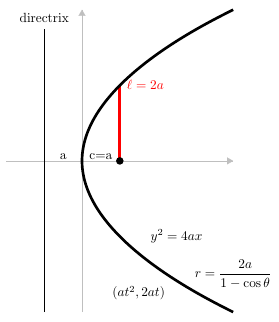
圓錐曲線的一般形式及其類型判定方法
圓錐曲線的一般形式為:
\[Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\]寫為矩陣的形式為:
\begin{equation} \begin{pmatrix} x & y \end{pmatrix} \begin{pmatrix} A & B/2 \newline B/2 & C \end{pmatrix} \begin{pmatrix} x \newline y \end{pmatrix} + \begin{pmatrix} D & E \end{pmatrix} \begin{pmatrix} x \newline y \end{pmatrix} + F = 0 \end{equation}
或者
\begin{equation} \begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} A & B/2 & D/2 \newline B/2 & C & E/2 \newline D/2 & E/2 & F\end{pmatrix} \begin{pmatrix} x \newline y \newline 1 \end{pmatrix} = 0 \end{equation}
判別式
令$\Delta = B^2 - 4AC$,則有:
若$B^2 - 4AC < 0$,則二次曲線為一橢圓;
- 若$ A= C, B = 0$,則曲線為一圓周;
若$B^2 - 4AC = 0$,則二次曲線為一拋物線;
若$B^2 - 4AC > 0$,則二次曲線為一雙曲線。
離心率為:
\(e = \sqrt{\dfrac{2\sqrt{(A-C)^2 + B^2}}{\eta(A+C) + \sqrt{(A-c)^2 + B^2}}}\) 如果上面的三階行列式取值小於零,則$\eta = 1$,若上面的三階行列式取值大於零,則$\eta = -1$.
一般方程如何標準化
對於橢圓和雙曲線的方程: \(Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0\) 通過變換可以化為以下形式 \begin{equation} \dfrac{x’^2}{-S/(\lambda_1^2\lambda_2)} + \dfrac{y’^2}{-S/(\lambda_1\lambda_2^2)} = 1 \end{equation}
這裡$\lambda_1, \lambda_2$為下述矩陣的特徵值:
$S$為上述三階矩陣的行列式。
參考文獻
Ayoub, A. B., “The central conic sections revisited”, Mathematics Magazine 66(5), 1993, 322–325.
https://en.wikipedia.org/wiki/Conic_section
