今天簡單談談矩陣(Matrix)和行列式(Determinant)。
矩阵Matrix
中文中矩陣的概念最早見於1922年。1922年,北京師範大學附屬中學數學老師程廷熙在 一篇介紹文章中將矩陣譯為「縱橫陣」。1925年,科學名詞審查會算學名詞審查組在《科學》 第十卷第四期刊登的審定名詞表中,矩陣被翻譯為「矩陣式」,方塊矩陣翻譯為「方陣式」, 而各類矩陣如「正交矩陣」、「伴隨矩陣」中的「矩陣」則被翻譯為「方陣」。1935年,中國 數學會審查後,中華民國教育部審定的《數學名詞》(並「通令全國各院校一律遵用,以昭劃一」) 中,「矩陣」作為譯名首次出現。1938年,曹惠群在接受科學名詞審查會委託就數學名詞加以校訂 的《算學名詞彙編》中,認為應當的譯名是「長方陣」。中華人民共和國成立後編訂的《數學名詞》 中,則將譯名定為「(矩)陣」。1993年,中國自然科學名詞審定委員會公布的《數學名詞》中, 「矩陣」被定為正式譯名,並沿用至今[1]。
矩陣作為線性方程組的工具,有很長的歷史。矩陣出現在行列式後。
《九章算術》出現以矩陣表示線性方程組係數來解方程;
日本數學家關孝和(1683年)與微積分的發現者之一戈特弗里德·威廉·萊布尼茨(1693年)近乎同 時地獨立建立了行列式論。
奧古斯丁·路易·柯西是最早將行列式排成方陣並將其元素用雙重下標表示的數學家。詹姆斯·約瑟 夫·西爾維斯特注意到,在作為行列式的計算形式以外,將數以行和列的形式作出的矩形置換本身也 是值得研究的。在他希望引用數的矩形陣列而又不能用行列式來形容的時候,就用「matrix」一詞 來形容。
阿瑟·凱萊被公認為矩陣論的奠基人。
後續發展:埃爾米特證明了如果矩陣等於其複共軛轉置,則特徵根為實數。1878年,弗比尼斯給出了 正交矩陣、相似矩陣和合同矩陣的概念。1906年,希爾伯特引入無限二次型(相當於無限維矩陣) 對積分方程式進行研究。
矩陣:將一些元素置換成若干行,每行放置相同的元素,就是一個矩陣。例如:
$\left[\begin{array}{ccc} 9 & 13 & 5 \newline 1 & 11 & 7 \newline 3 & 9 & 2 \newline 6 & 0 & 7 \end{array}\right]$ 行數是1或者列數是1的矩陣分別稱為行向量和列向量。
線性方程組的矩陣表示:
$ \begin{cases}a_{1,1}x_{1} + a_{1,2}x_{2} + \cdots + a_{1,n}x_{n}= b_{1} \newline a_{2,1}x_{1} + a_{2,2}x_{2} + \cdots + a_{2,n}x_{n}= b_{2} \newline \vdots \quad \quad \quad \vdots \newline a_{m,1}x_{1} + a_{m,2}x_{2} + \cdots + a_{m,n}x_{n}= b_{m} \end{cases} $ 可以表示為:
$\mathbf{A}\mathbf{x} = \mathbf{b}$ 其中,
$\mathbf{A} = \begin{bmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \newline a_{2,1} & a_{2,2} & \cdots & a_{2,n} \newline \vdots & \vdots & \ddots & \vdots \newline a_{m,1} & a_{m,2} & \cdots & a_{m,n} \end{bmatrix},\quad \mathbf{x} = \begin{bmatrix} x_1 \newline x_2 \newline \vdots \newline x_n \end{bmatrix},\quad \mathbf{b} = \begin{bmatrix} b_1 \newline b_2 \newline \vdots \newline b_m \end{bmatrix}$
行列式
行列式為數學中的一個函數,該函數將一個$n \times n$的矩陣影射到一個數, 記作$\mathrm{det}(\mathbf{A})$或者$\vert \mathbf{A} \vert$。行列式可以看成是有向面積或者 體積的概念在歐幾里德空間的推廣。
二階行列式
設
$\mathbf{A} = \begin{bmatrix} 1 & 3 \newline 2 & 10\end{bmatrix}$ 則,$\vert A \vert = 1 \times 10 - 3 \times 2 = 4$
對於一個二階矩陣:
$\mathbf{A} = \begin{bmatrix} a & b \newline c & d\end{bmatrix}$ 則,$\vert A \vert = a \times d - b \times c $
下圖表示二階矩陣的運算,藍色為正$ad$,紅色為負$-bc$。

幾何意義
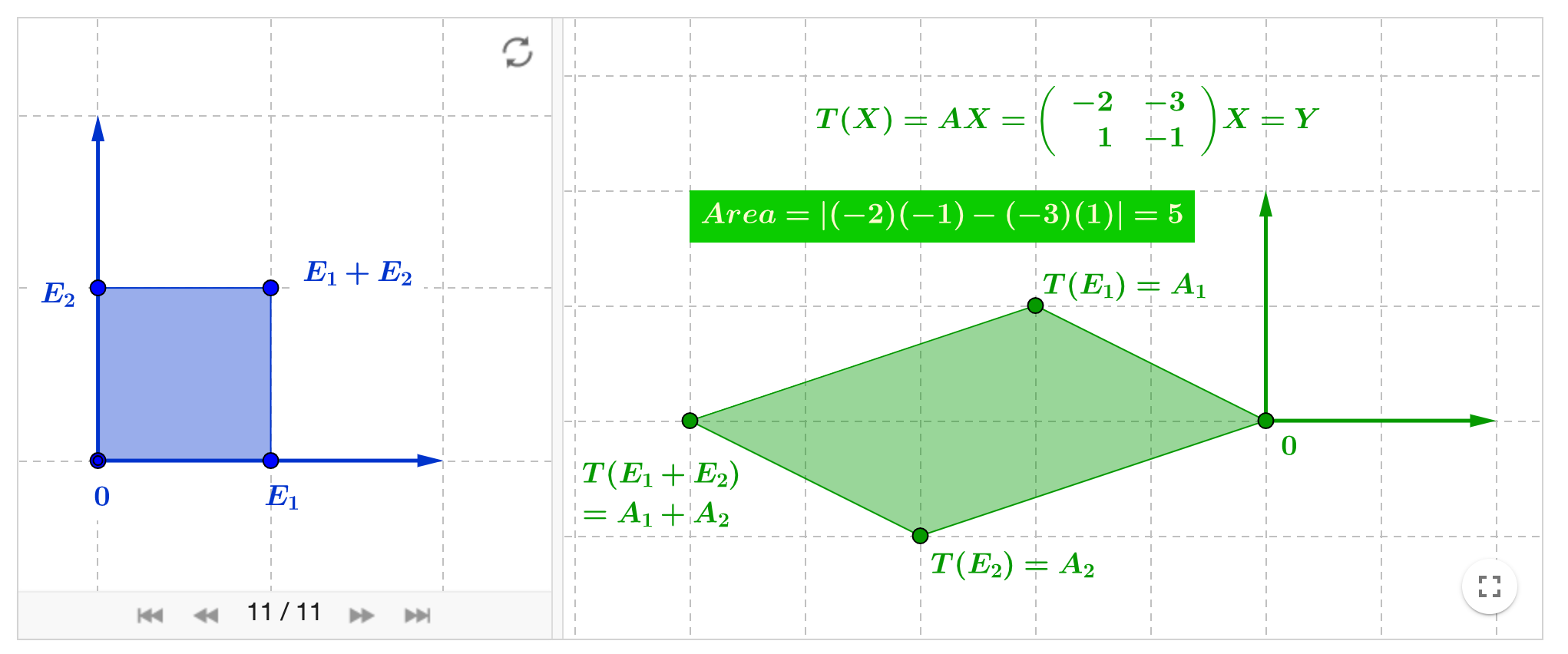
解線性方程組克萊姆法則:

三階行列式
設
$\mathbf{A} = \begin{bmatrix} a & b & c \newline d & e & f \newline g & h & i\end{bmatrix}$ 則
$\vert \mathbf{A} \vert = a \times (e \times i - f \times h) - b \times (d \times i - f \times g) + c \times (d \times h - e \times g)$ 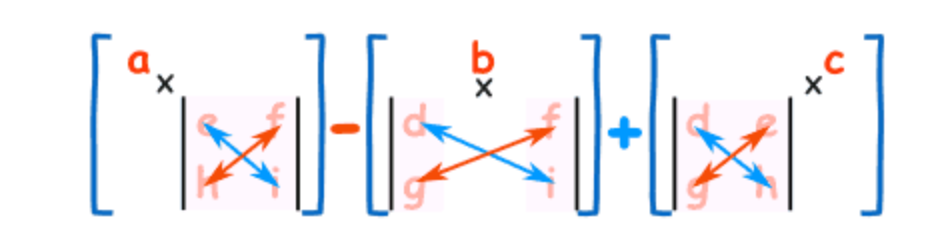
例如:
$\mathbf{A} = \begin{bmatrix} 6 & 1 & 1 \newline 4 & -2 & 5 \newline 2 & 8 & 7\end{bmatrix}$ 則
$\vert \mathbf{A} \vert = 6 \times (-2 \times 7 - 5\times 8) - 1 \times (4 \times 7 - 5 \times 2) + 1 \times (4 \times 8 - (-2) \times 2) = -306$
四階行列式
設
$\mathbf{A} = \begin{bmatrix} a & b & c & d \newline e & f & g & h \newline i & j & k & l \newline m & n & o & p\end{bmatrix}$ 則
$ \vert \mathbf{A} \vert = a \times \begin{bmatrix} f & g & h \newline j & k & l \newline n & o & p \end{bmatrix} - b \times \begin{bmatrix} e & g & h \newline i & k & l \newline m & o & p \end{bmatrix} + c \times \begin{bmatrix} e & f & h \newline i & j & l \newline m & n & p \end{bmatrix} - d \times \begin{bmatrix} e & f & g \newline i & j & k \newline m & n & o \end{bmatrix} $ 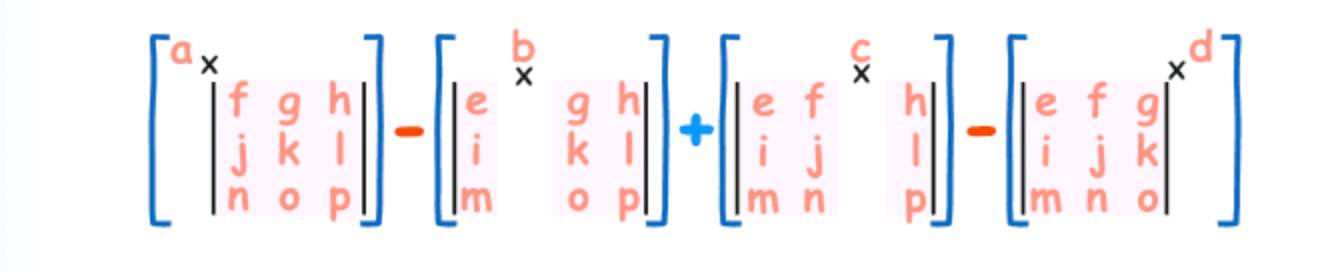
👏 THANKS











