Dropout: a Regularization Method for Deep Learning

This talk is about the regularization methods in deep learning.

Introduction

Deep neural networks contain multiple non-linear hidden layers and this makes them very expressive models that can learn very complicated relationships between their inputs and outputs. With limited data, however, many of these complicated relationships will be the result of sampling noise, so they will exist in the training set but not in real test data even if it is drawn from the same distribution. This leads to overfitting and many methods have been developed for reducing it. These including:

• Stopping the training as soon as performance on a validation set starts to get wrose;
• Introducing weight penalties of various kinds such as:
  • $L1$ regularization;
  • $L2$ regularization;
  • Soft weight sharing;
  • Dropout method.

Why does Dropout can prevent over-fitting?

1. Average Effect A neural network with $n$ units, can be seen as a collection of $2^n$ possible thinned neural network:

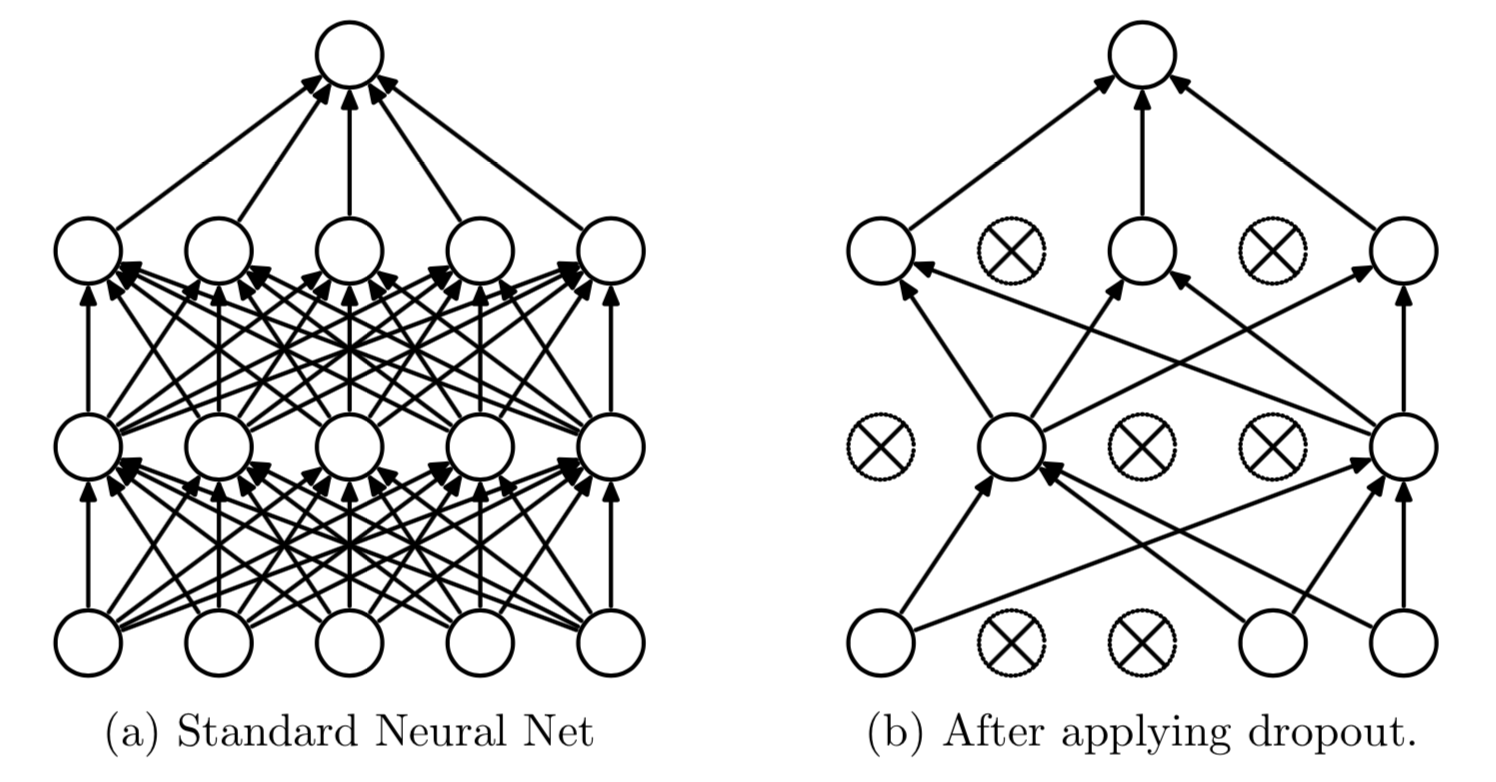
With unlimited computation, the best way to “regularize” a fixed-sized model is to average the predictions of all possible settings of the parameters, weighting each setting by its posterior probability given the training data. This can sometimes be approximated quite well for simple or small models (Xiong et al., 2011; Salakhutdinov and Mnih, 2008), but we would like to approach the performance of the Bayesian gold standard using considerably less computation. We propose to do this by approximating an equally weighted geometric mean of the predictions of an exponential number of learned models that share parameters. In order to make neural net models different, they should either have different architectures or be trained on different data. Training many different architectures is hard because finding optimal hyper-parameters for each architecture is a daunting task and training each large network requires a lot of computation.

1. Sex of Evolution Sexual reproduction involves taking half the genes of one parent and half of the other, adding a very small amount of random mutation, and combining them to produce an offspring. One possible explanation for the superiority of sexual reproduction is that, over the long term, the criterion for natural selection may not be individual fitness but rather mix-ability of genes. The ability of a set of genes to be able to work well with another random set of a small number of other genes. Similarly, each hidden unit in a neural network trained with dropout must learn to work with a randomly chosen sample of other units.
2. Successful Conspiracies Ten conspiracies each involving five people is probably a better way to create havoc than one big conspiracy that requires fifty people to all play their parts correctly.
3. Stochastic Regularization Technique In simple cases, dropout can be analytically marginalized out to obtain deterministic regularization methods.

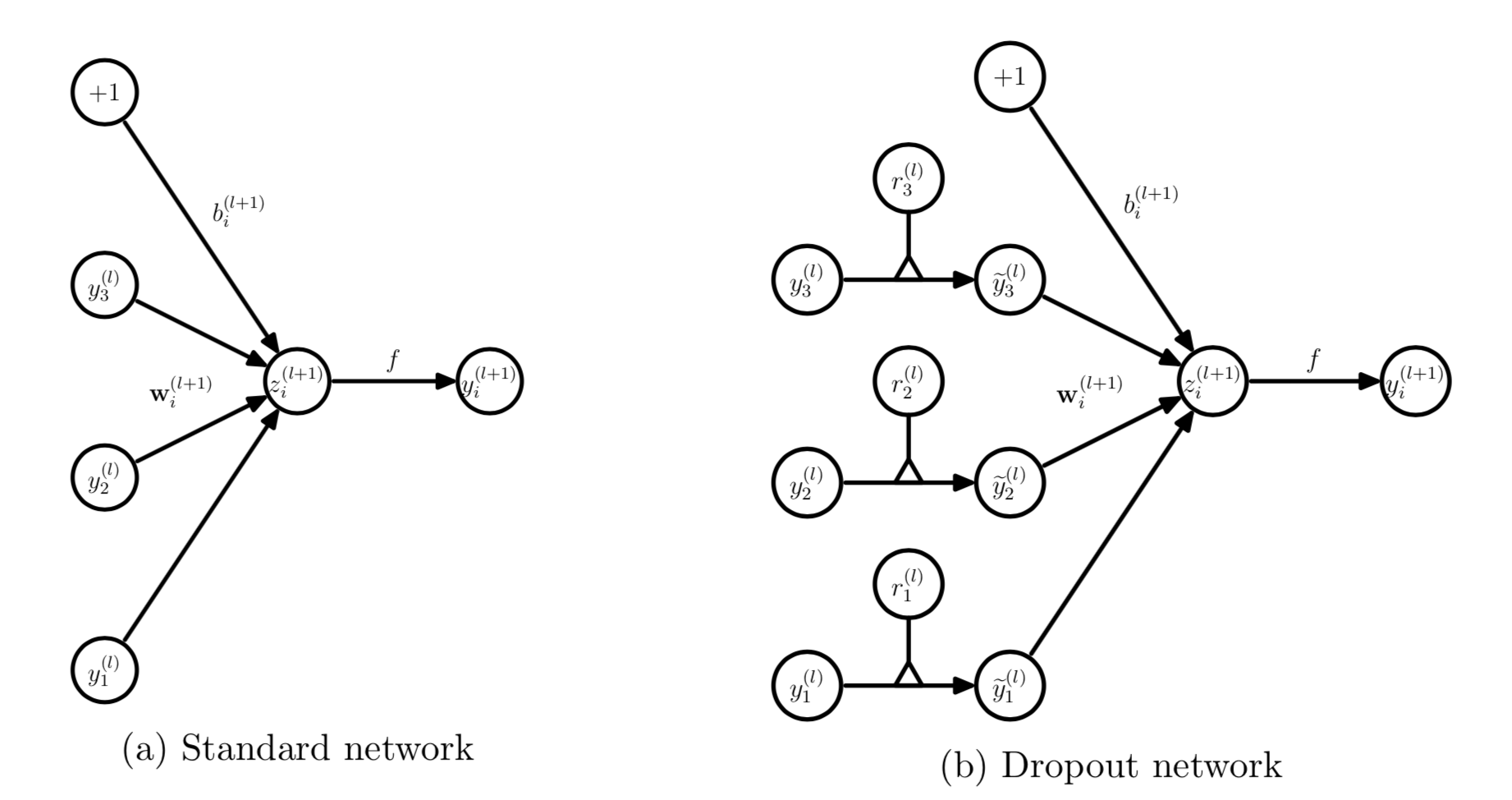
Model Description

The feed-forward operation of a standard neural network (Figure a) can be described as (for $l \in {0, \cdots, L-1}$) and any hidden unit $i$ \begin{equation} z_i^{(l+1)} = \mathbf{w}_i^{(l+1)}\mathbf{y}^l + b_i^{(l+1)}, \quad y_i^{(l+1)} = f\left(z_i^{(l+1)}\right) \label{eq:dropout1} \tag{1} \end{equation}

With dropout, the feed-forward operation becomes \begin{equation} r_j^{(l)} \sim \text{Bernoulli(p)}, \quad \widetilde{\mathbf{y}}^{(l)} = \mathbf{r}^{(l)} \mathbf{y}^{(l)},\quad z_i^{(l+1)} = \mathbf{w}_i^{(l+1)}\widetilde{\mathbf{y}}^l + b_i^{(l+1)},\quad y_i^{(l+1)} = f\left(z_i^{(l+1)}\right) \label{eq:dropout2} \tag{2} \end{equation}

Simple Code for Dropout

# coding:utf-8
import numpy as np

def dropout(x, level):
    if level < 0. or level >= 1: 
        raise ValueError('Dropout level must be in interval [0, 1[.')
    retain_prob = 1. - level

    random_tensor = np.random.binomial(n=1, p=retain_prob, size=x.shape) 
    print(random_tensor)

    x *= random_tensor
    print(x)
    x /= retain_prob
    print(x)

    return x

x=np.asarray([1,2,3,4,5,6,7,8,9,10],dtype=np.float32)
dropout(x,0.5)

Reference

[1]. Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: A simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958.

[2]. Dropout as data augmentation.