这部分介绍多元函数微分及其应用。

目录

• 第一节 平面点集与多元函数
• 第二节 二元函数的极限
• 第三节 二元函数的连续
• 第四节 二元函数可微性
• 第五节 方向导数与梯度
• 第六节 复合函数求导法则
• 第七节 隐函数求导法则
• 第八节 多元函数微分几何应用
• 第九节 极值与拉格朗日乘数法

📌1. 平面点集与多元函数

多元函数是指自变量为两个或两个以上的函数。作为一元函数的推广，自身保留了一元函数的许多性质，但是也产生了许多新的不同于一元函数的性质。本章主要针对于二元函数展开讨论，在掌握了二元函数的理论后可以推广到$n$元函数中去。

☘︎ 平面点集

当平面上确定一个坐标系后，所有的有序二元数组$(x,y)$与平面上的点之间建立了一一对应关系(数形对应)，这种确定了坐标系的平面称为坐标平面。

坐标平面上满足某些条件$P$的点的集合称为平面点集，记作

下图为平面上三个不同距离定义下的单位圆：

• 欧几里德距离: $Dist(P_1(x_1, y_1), P_2(x_2, y_2)) = \sqrt{(x_1 - x^2)^2 + (y_1 - y_2)^2}$;

• 切比雪夫距离: $Dist(P_1(x_1, y_1), P_2(x_2, y_2)) = \max \left(\vert x_1 - x_2 \vert, \vert y_1 - y_2\vert \right)$;

• 曼哈顿距离: $Dist(P_1(x_1, y_1), P_2(x_2, y_2)) = \vert x_1 - x_2\vert + \vert y_1 - y_2\vert$;

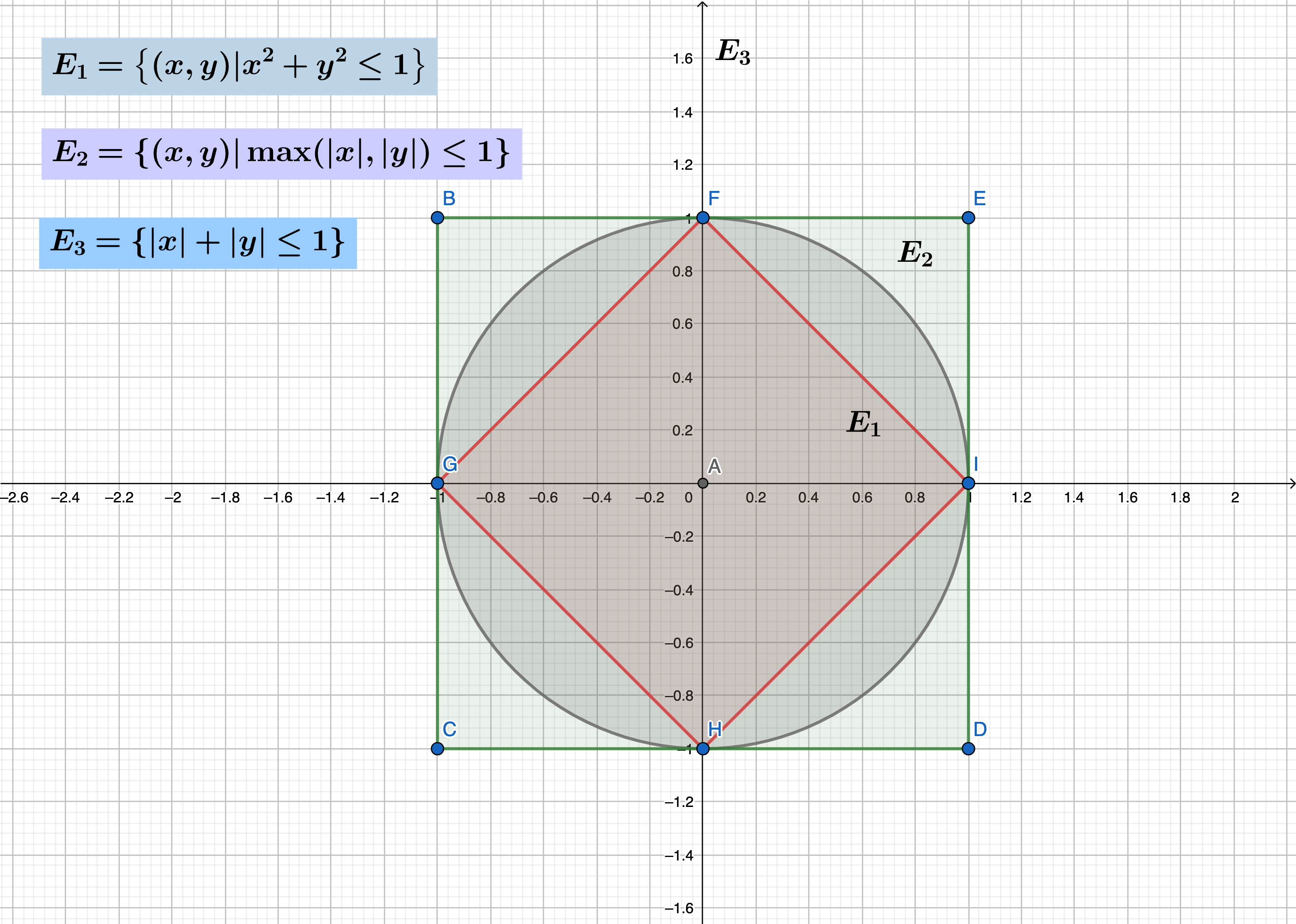
如果不作声明，我们一般🈯️欧几里德距离。

若$P(x_0, y_0) \in \mathbb{R}^2$，我们称到点$P_0$的距离小于$\delta$的所有点的集合称为$P_0$的$\delta$邻域，记作$U(P_0, \delta)$.

☘︎ 点集与集合之间的关系

假设$E \subset \mathbb{R}^2$, 有：

• 内点: 若存在点$P$的邻域$U(P)$，使得$U(P) \subset E$;

• 边界点: 若$P$的任何一个邻域既含有$E$中的点，又含有不属于$E$中的点；

• 外点: 若存在$P$的一个邻域$U(P)$，使得$U(P) \cap E = \emptyset$

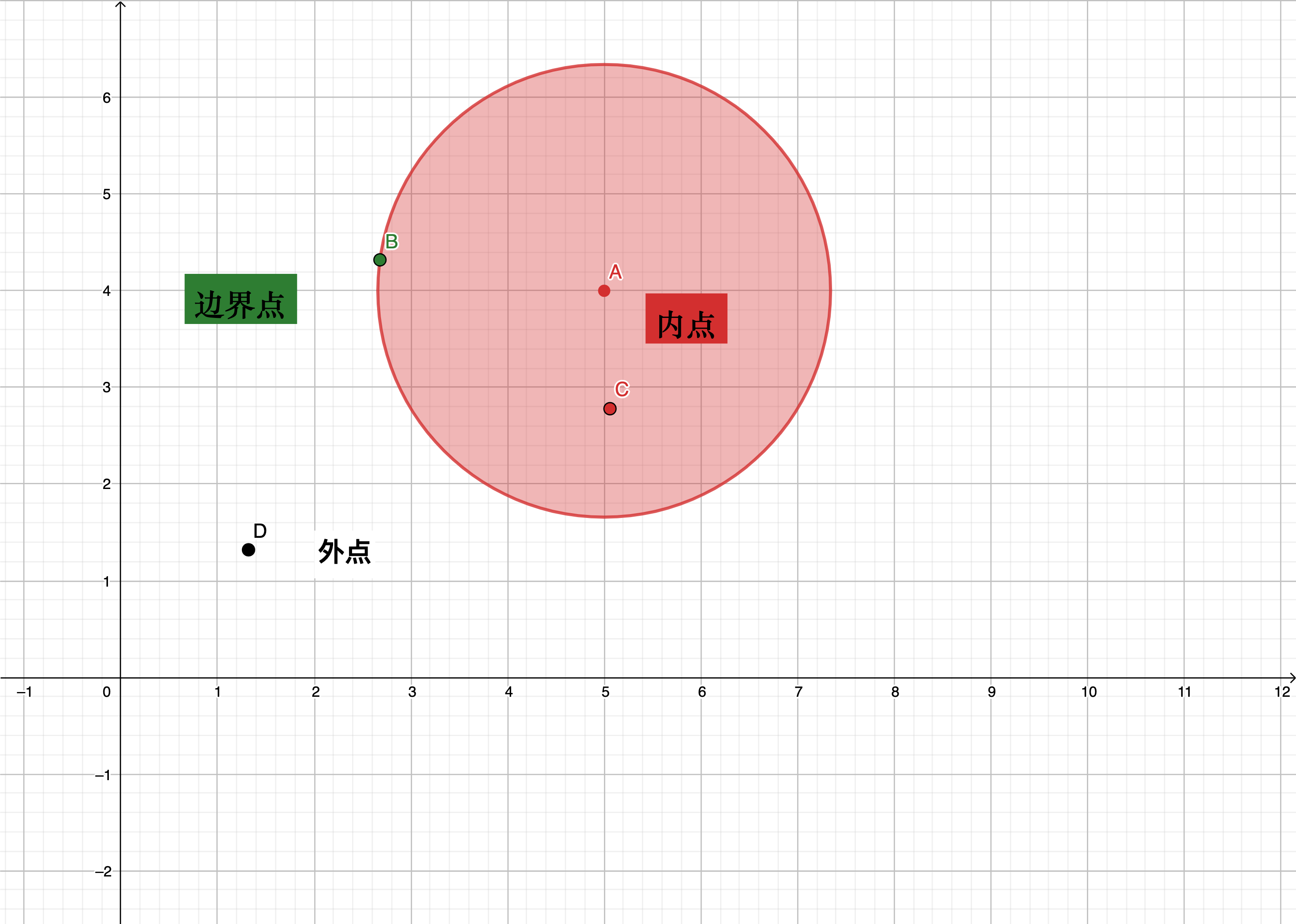
另外点$P$与集合$E$的另一种关系为：

• 聚点: 若点$P$的任何一个空心邻域$\mathring{U}(P, \delta)$都含有$E$中的点，则$P$称为$E$的聚点；

• 孤立点: 若$P \in E$但不是$E$的聚点。

☘︎ 一些重要的平面点集的定义

• 开集: 若平面点集$E$中的每一个点都为$E$的内点；

• 闭集: 若点集$E$中的所有聚点都属于$E$，或者$E^C$($E$的补集)为开集；

• 有界集: 若集合$E$中的点到$O(0,0)$的最大距离为一个有限数；

• 开域: 若非空开集合$E$具有连通性，即$E$中的任意两点都可以用属于$E$中的折线相连接；

• 闭域: 开域连同其边界形成的点集；

• 区域: 开域、闭域、或者开域连同一部分边界点形成的点集。

☘︎ 二元函数

设$D \subset \mathbb{R}^2$，若按照某个对应法则$f$，$D$中的每一个点$P(x,y)$都有一个确定的实数$z$与之对应，则称$f$ 为定义在$D$上的一个二元函数，记作

称$D$为$f$的定义域。若$P \in D$称与$P$所对应的$z$为点$P$的函数值，记为$z = f(P)$。全体函数值的集合为$f$的值域。$(x,y)$称为$f$的自变量，而把$z$称为因变量。

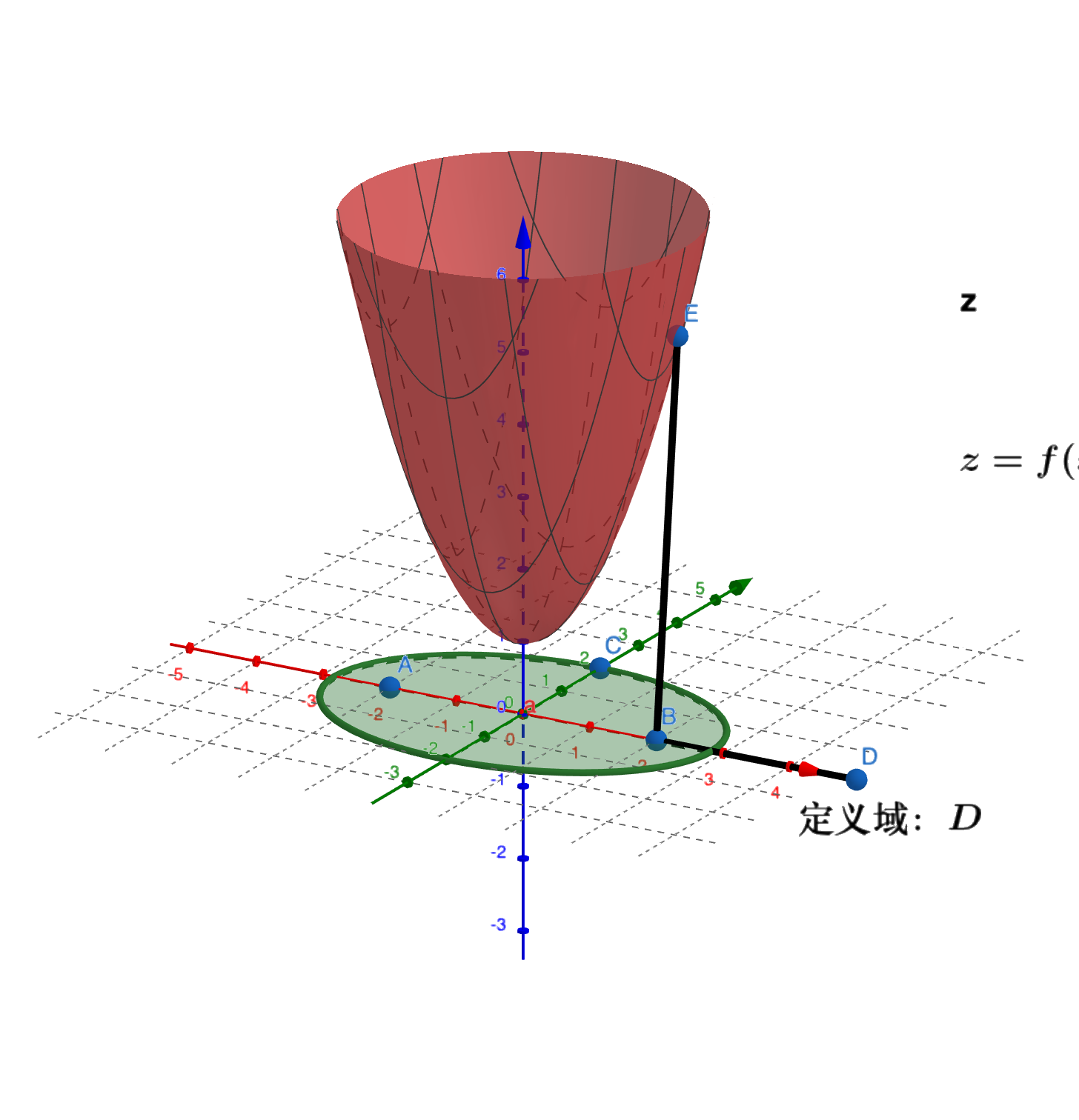
☘︎ $n$元函数

设$D \subset \mathbb{R}^n$，若按照某个对应法则$f$，$D$中的每一个点$P(x_1, x_2, \cdots, x_n)$都有一个确定的实数$z$与之对应，则称$f$ 为定义在$D$上的一个$n$元函数，记作

例子

• 显示二元函数

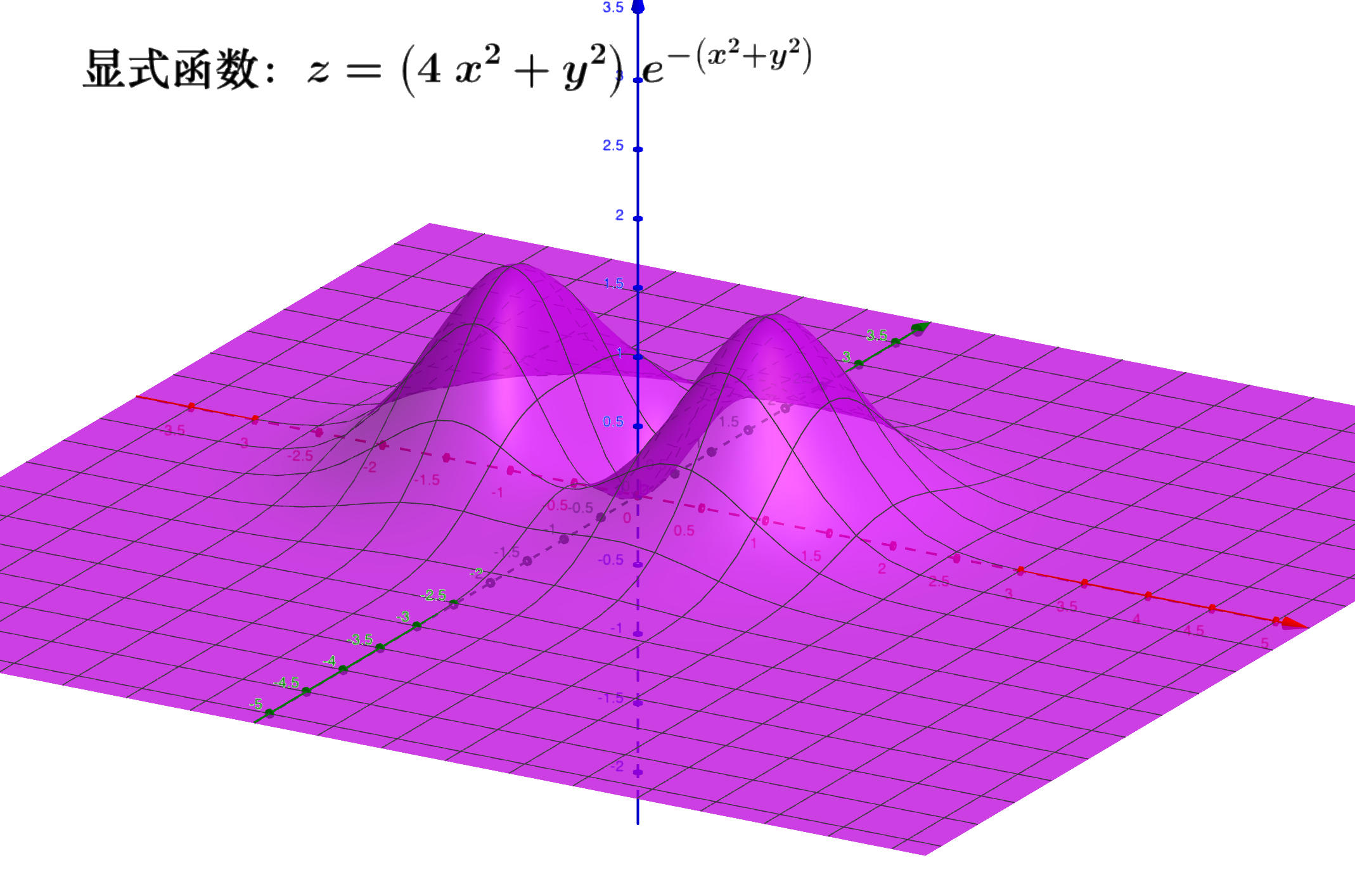
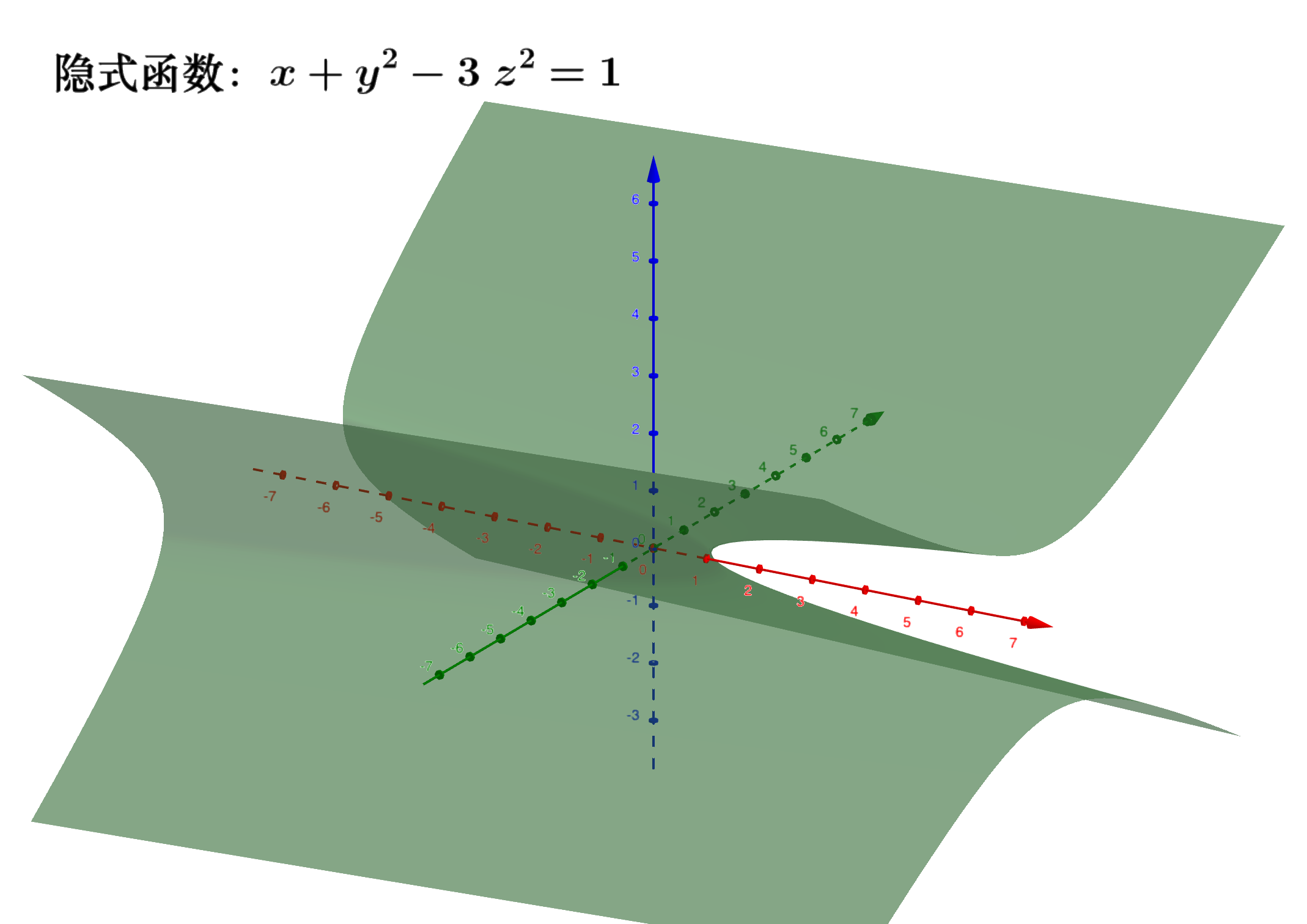
• 隐式函数

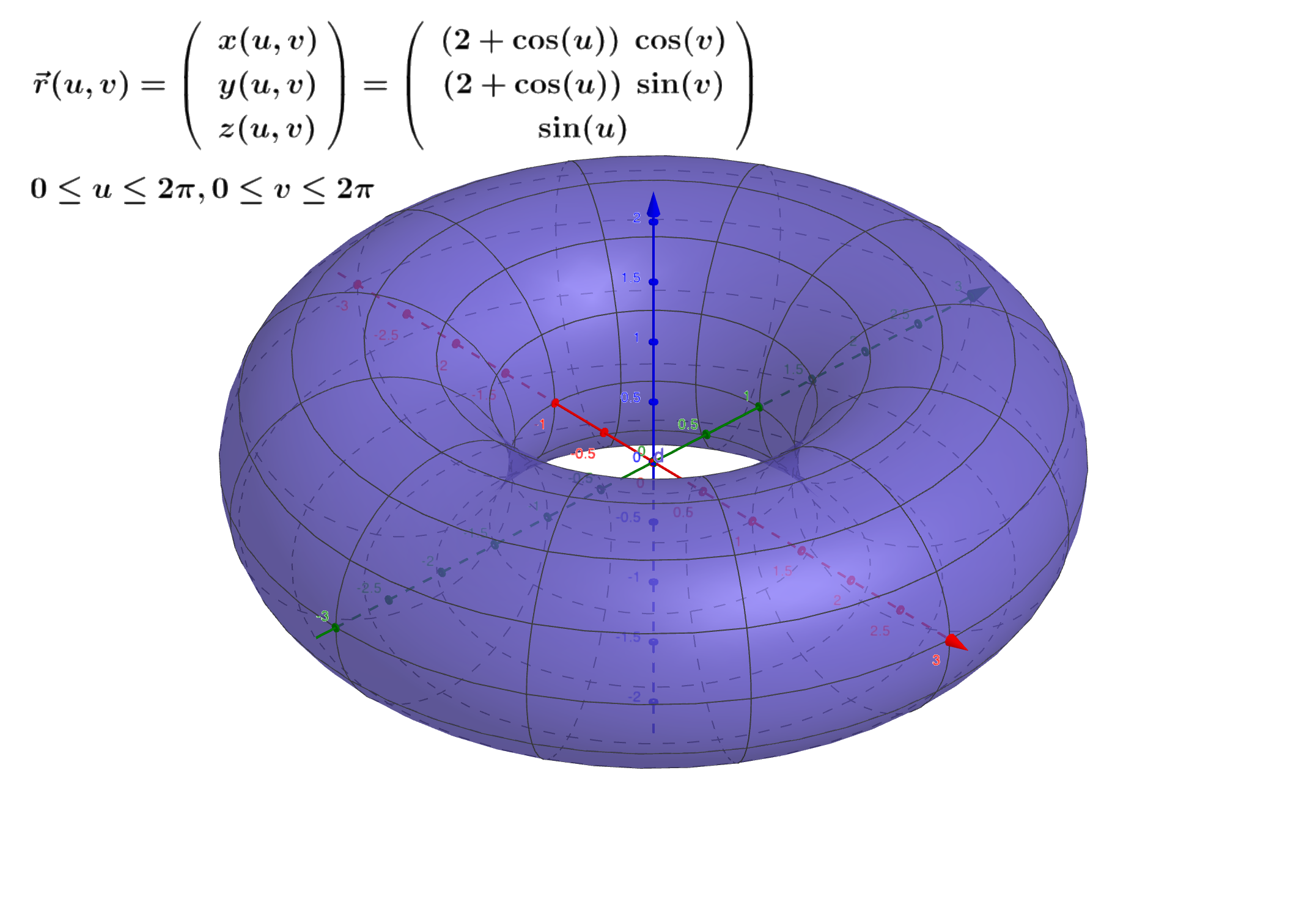
• 参数方程

📚第一次作业:

• 求下列函数的定义域：

  • $f(x,y) = \sqrt{x^2 + y^2}$

  • $f(x, y) = \ln (y - x)$

  • $f(x, y) = \sqrt{R^2 - x^2 - y^2} + \dfrac{1}{\sqrt{x^2 + y^2 - r^2}}(R > r)$

📌2. 二元函数的极限

设二元函数$f(x,y)$的定义域为$D \subset \mathbb{R}^2$, $P_0$为$D$的一个聚点，$A$是一个确定的实数。如果对于任意的$\epsilon > 0$，总存在某一个正数$\delta > 0$，使得当$P \in \mathring{U}(P_0, \delta)$时($0 < |P - P_0| < \delta$)时，有$\vert f(P) - A \vert < \epsilon$。则称$f(x, y)$当$P \to P_0$时极限为$A$，记为：

数学逻辑语言为:

✏️例子

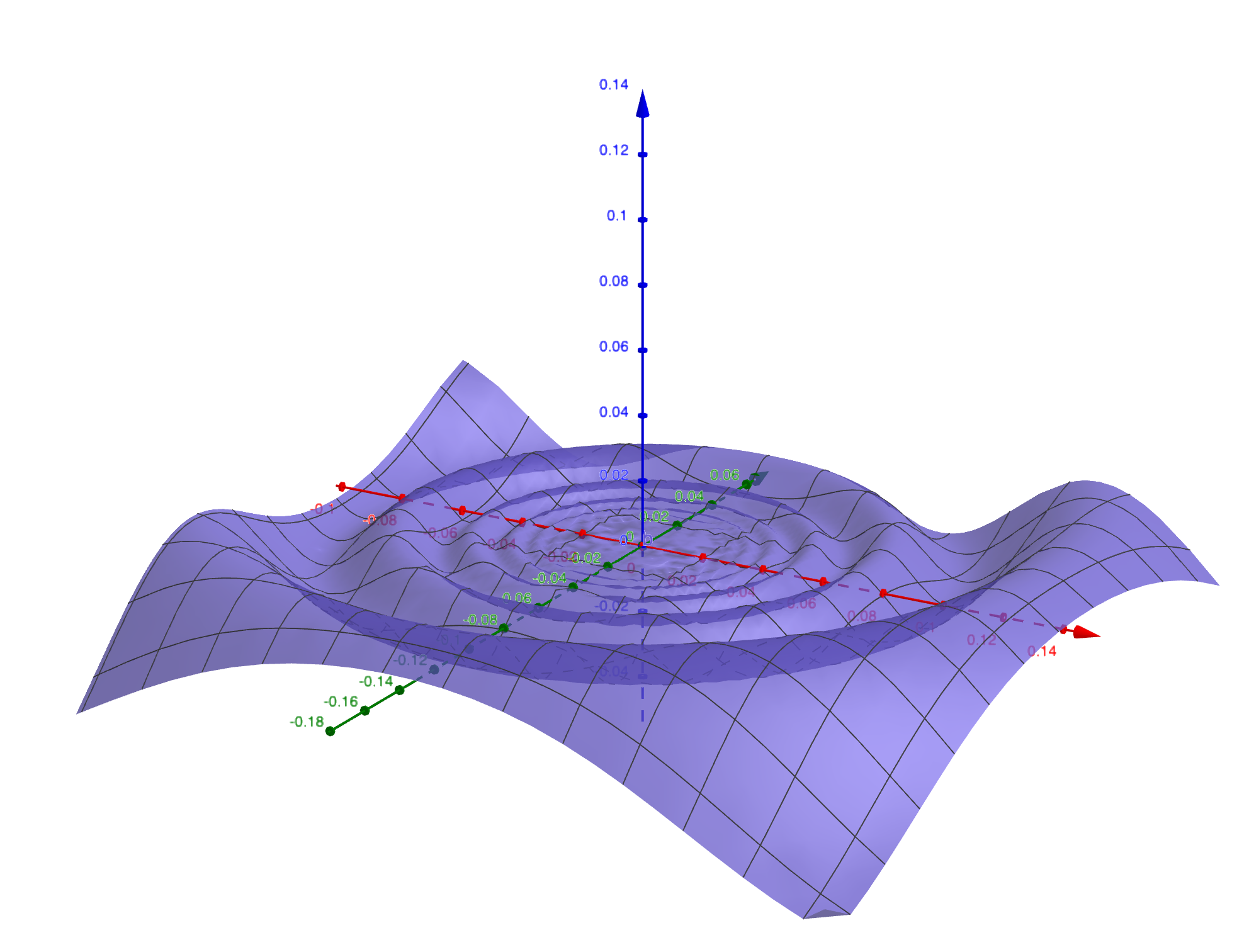
设$f(x,y) = (x^2 + y^2)\sin \dfrac{1}{\sqrt{x^2 + y^2}}$，证明$\lim\limits_{(x,y) \to (0,0)} f(x,y) = 0$

✏️例子

讨论极限$\lim\limits_{(x, y) \to (0, 0)} \dfrac{xy}{x^2 + y^2}$

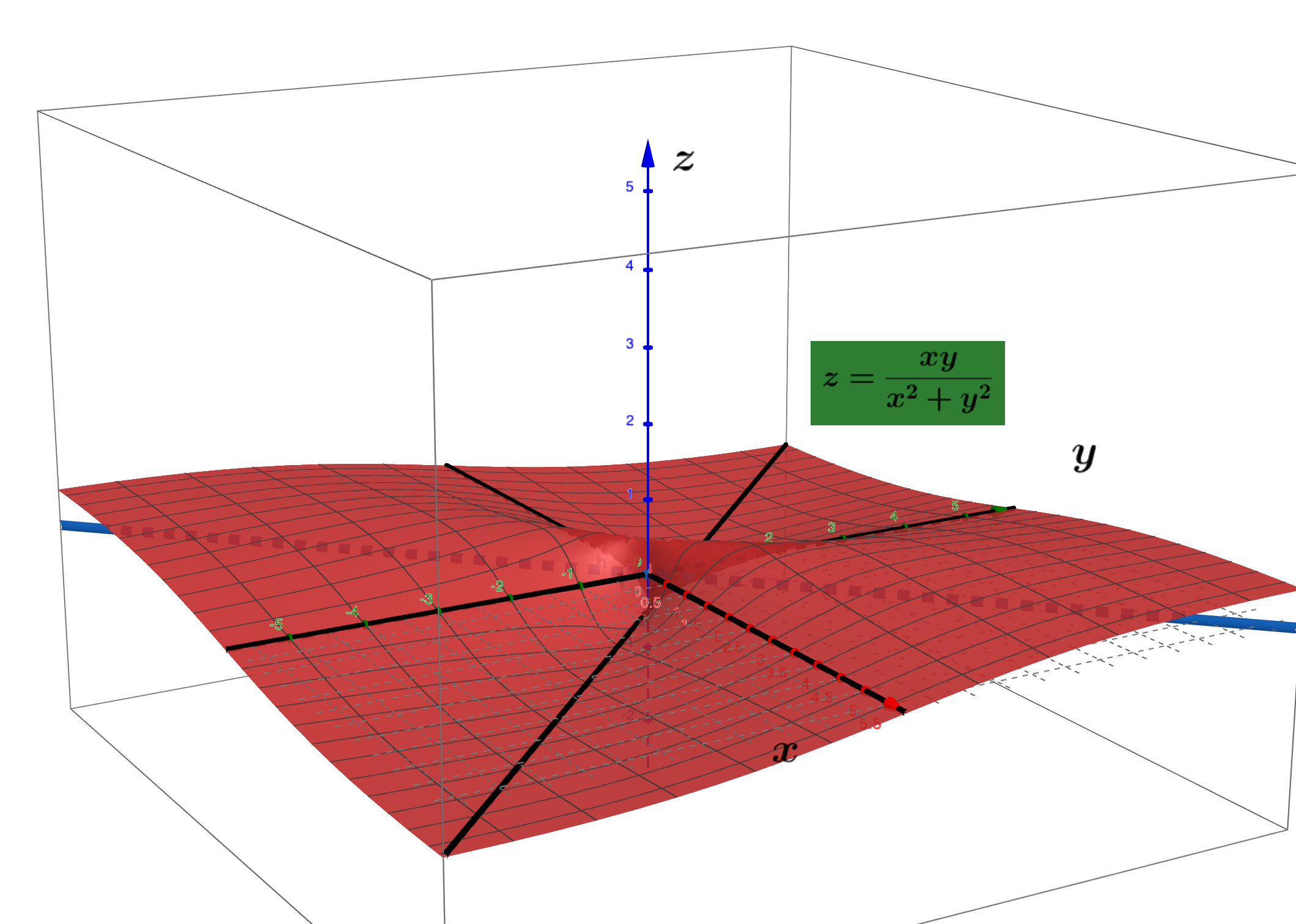
✏️例子

讨论极限$\lim\limits_{(x, y) \to (0, 0)} \dfrac{x^2 + y^2}{\sqrt{x^2 + y^2 + 1} - 1}$

⬇️ Click to expand!

解： $ \begin{split} \lim\limits_{(x, y) \to (0, 0)} \dfrac{x^2 + y^2}{\sqrt{1 + x^2 + y^2} - 1} & = \lim\limits_{t \to 0}\dfrac{t}{\sqrt{(1 + t) - 1}}\newline & \lim\limits_{t \to 0}\dfrac{t}{1/2 t} = 2. \end{split} $

– 例子

• 求极限夹击准则法：

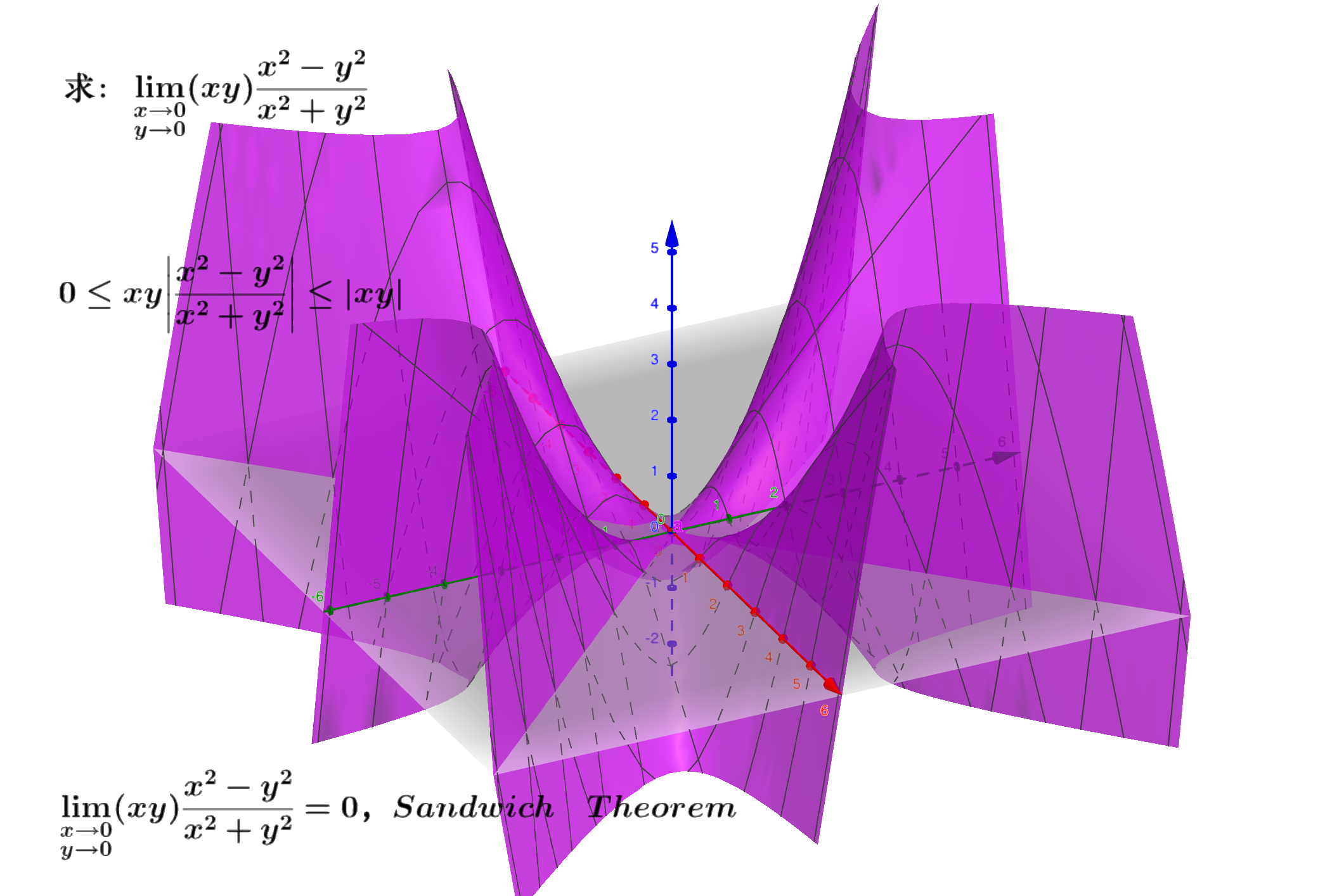
• 求极限极坐标法：

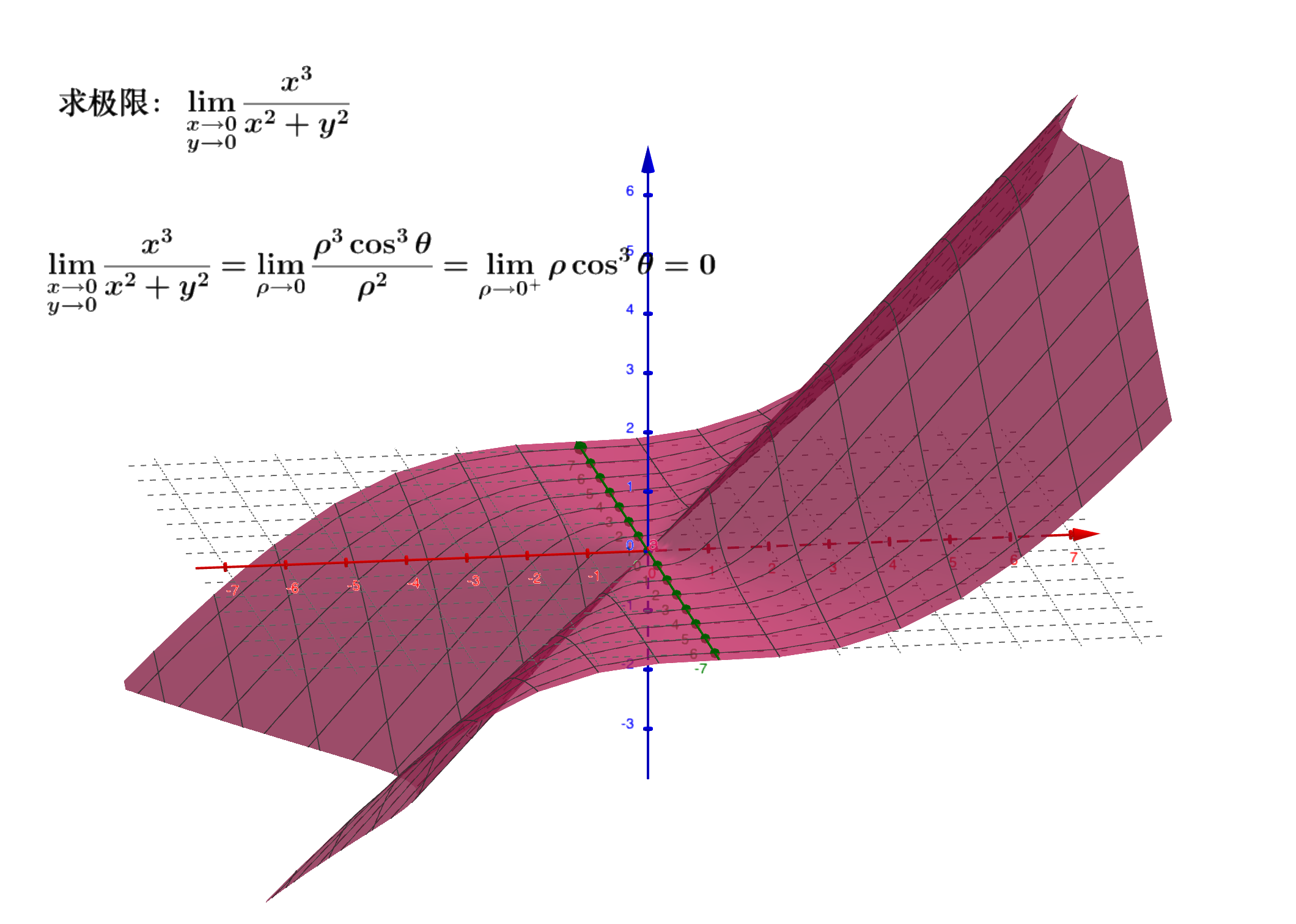
☘︎ 累次极限

几种极限：

• 重极限：$\lim\limits_{(x,y) \to (x_0, y_0)} f(x,y)$;

• 累次极限：$\lim\limits_{x \to x_0}\lim\limits_{y \to y_0} f(x, y)$ 或者 $\lim\limits_{y \to y_0}\lim\limits_{x \to x_0}f(x, y)$

🛠思考题

思考重极限和累次极限的关系是什么？

📚第二次作业:

• 求下列极限

  • $\lim\limits_{(x,y) \to (0, 1)}\dfrac{1 - xy}{x^2 + y^2}$;

  • $\lim\limits_{(x,y) \to (0, 0)}\dfrac{2 - \sqrt{4 + xy}}{xy}$;

  • $\lim\limits_{(x,y) \to (0, 0)}\dfrac{x + y}{x - y}$

• 函数$z = \dfrac{y^2 + 2x}{y^2 - 2x}$在何处间断？

📌3. 二元函数的连续

☘︎ 二元函数连续性定义

设函数$f$为定义在点集$D \subset \mathbb{R}^2$上的二元函数，$P_0 \in D$(它或者是$D$的聚点，或者是$D$的孤立点)，对于任意的$\epsilon > 0$，总存在相应的$\delta > 0$，只要$P \in U(P_0, \delta) \cap D$，有：

则称$f$在$P_0$点连续。

数学逻辑语言为:

☘︎ 连续函数的性质

有界闭区域上的连续函数有以下性质：

• 有界性、能够取得最大最小值；

• 介值定理；

• 一致连续。

📚第三次作业:

• 讨论下列函数的连续性：

  • $f(x, y) = \lfloor x + y \rfloor$(取整函数)；

  • $f(x, y) = \left\{\begin{array}{cl} \dfrac{\sin xy}{\sqrt{x^2 + y^2}}, & x^2 + y^2 \ne 0 \newline 0, & x^2 + y^2 = 0 \end{array} \right. $

📌4. 二元函数可微性

☘︎ 可微与全微分

在一元函数中，函数可微的几何意义为函数在给定点的切线存在，函数在给定点处的微分其实为函数对应点的线形映射。

设函数$z = f(x, y)$在$P(x_0, y_0)$点的某邻域$U(P_0)$上有定义，对于$P(x_0 + \Delta x, y_0 + \Delta y) \in U(P_0)$，如果有：

其中$A, B$仅与$P_0$有关，$\rho = \sqrt{\Delta x^2 + \Delta y^2}$，$o(\rho)$为$\rho$的高阶无穷小量(第二种情形，$\epsilon_1, \epsilon_2$为随着$\Delta x, \Delta y \to 0$的无穷小量)，则称函数$f$在$P_0$点可微，并称线性函数$A\Delta x + B\Delta y$为函数$f$的全微分，记作：

例子

考察函数$f(x,y) = 3x+4y+2$在$(x_0, y_0)$处的可微性。

例子

考察函数$f(x,y) = xy$在$(x_0,y_0)$处的可微性。

☘︎ 偏导数

对于二元函数，固定其中的一个变量，考察二元函数对其中一个变量的变化率，这就是偏导数。

设函数$z = f(x,y), (x,y) \in D$，若$(x_0, y_0) \in D$，且$f(x, y_0)$在$x_0$的某邻域内有定义，则当极限

存在时，称这个极限为函数$f$在$(x_0,y_0)$关于$x$的偏导数， 记作

同样可以定义$f$关于点$(x_0, y_0)$关于$y$的偏导数$f_y(x_0, y_0), \left.\dfrac{\partial f}{\partial y}\right\vert_{(x_0,y_0)}$

二元函数偏导数$f_x(x_0, y_0)$是曲面$z = f(x, y)$与平面$y = y_0$的交线在$x = x_0$点的导数。

关于偏导数的几何意义，见下图：

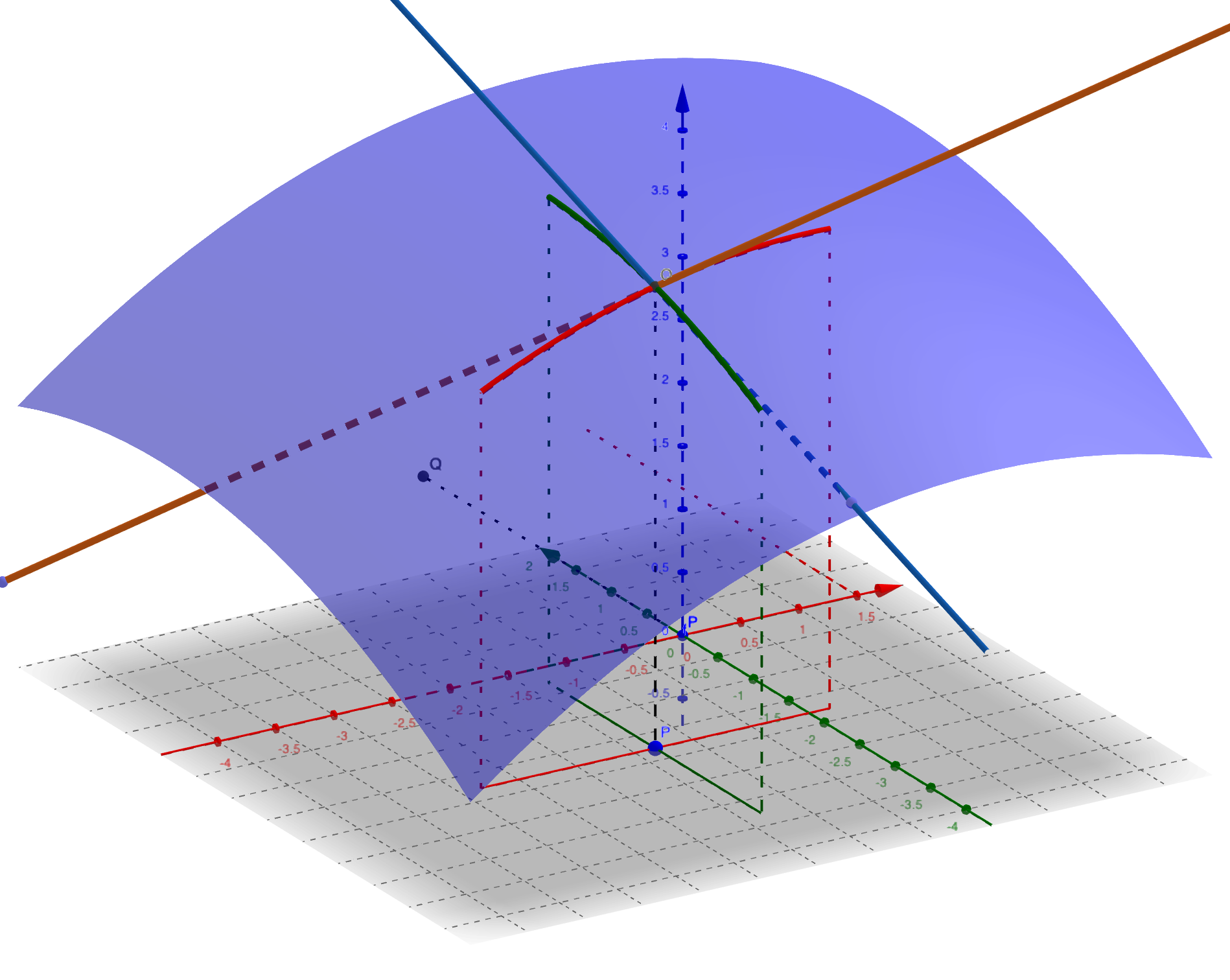
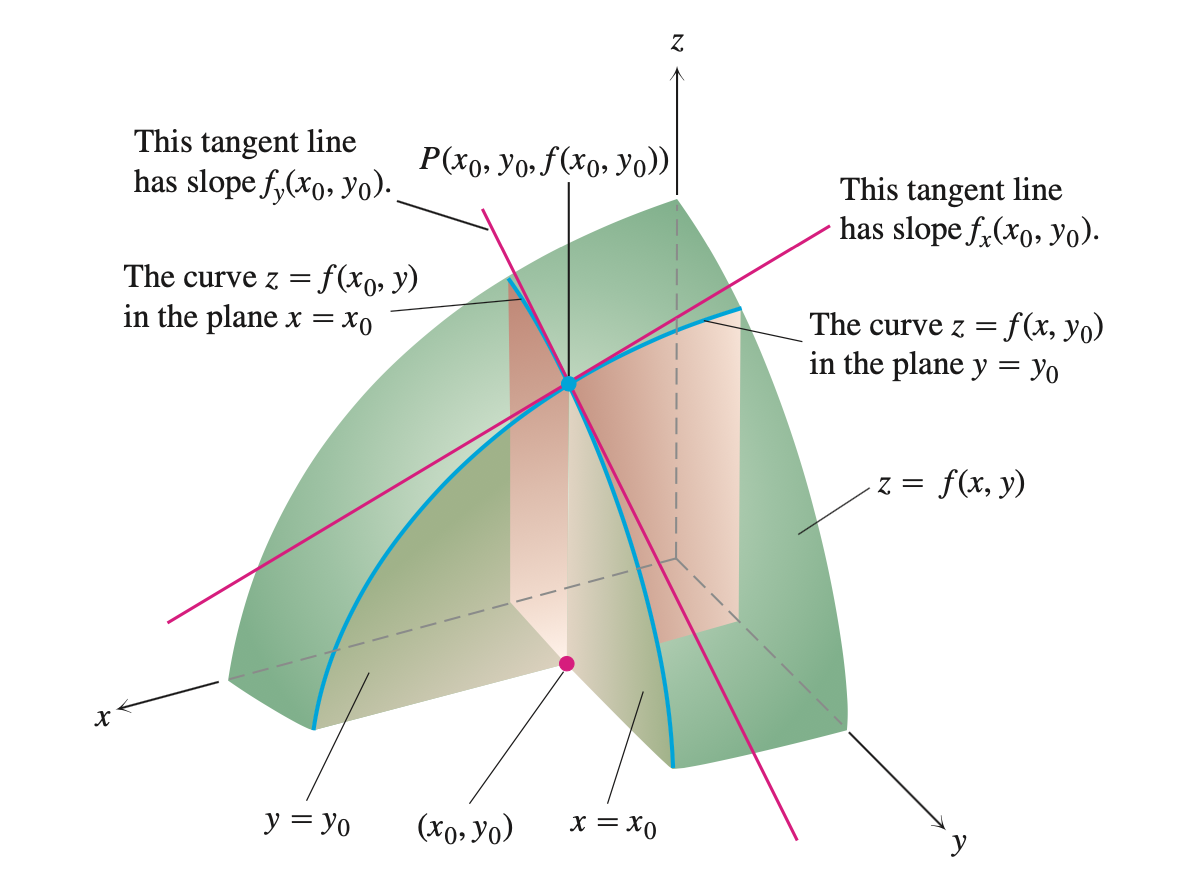
若函数$z = f(x,y)$在区域$D$上的每一点$(x,y)$都存在对$x$(或对$y$)的偏导数，则得到函数$z = f(x, y)$在区域$D$上对$x$(或对$y$)的偏导函数，记作

✏️例子

求函数$f(x, y) = x^3 + 2x^2y - y^3$在点$(1,3)$关于$x$和关于$y$的偏导数。

python code

s = "Python syntax highlighting"

# import modules
import sympy as sym

# Define the symbol function
x, y = sym.symbols('x y')
f = x**3 + 2*x**2*y - y**3
f_x = sym.diff(f, x)
f_x = sym.diff(f, y)

# Compute the values
f_x.subs([(x,1),(y,3)])
f_y.subs([(x,1),(y,3)])

☘︎ 高阶偏导数

对一阶偏导函数求偏导数，或者是对函数求两次偏导数得到函数的二阶偏导数。二阶偏导数记作，

这里二阶偏导数的计算过程为：

✏️例子 设$z = x^3y^2 - 3xy^3 - xy + 1$求 $\dfrac{\partial^2 z}{\partial x^2}, \dfrac{\partial^2 z}{\partial x \partial y}$

如果函数$z = f(x,y)$的两个混合偏导数$\dfrac{\partial f}{\partial x \partial y}, \dfrac{\partial^2f}{\partial y \partial x}$连续，则两个混合偏导数相等。

☘︎ 可微、连续和偏导的关系探讨

• 可微: $P(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0) = A\Delta x + B\Delta y + \epsilon_1 \Delta x + \epsilon_2 \Delta y$;

• 连续: $\lim\limits_{(\Delta x, \Delta y) \to (0, 0)}f(x_0 + \Delta x, y_0 + \Delta y) = f(x_0, y_0)$;

• 偏导数存在：$\lim\limits_{\Delta x \to 0 }\dfrac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} = 存在$ 和 $\lim\limits_{\Delta y \to 0 }\dfrac{f(x_0, y_0 + \Delta y) - f(x_0, y_0)}{\Delta y} = 存在$

💡可微===>连续，但是连续不一定可微。

如果函数$f$在$P_0(x_0, y_0)$点可微，则有：

在上面等式中令$\Delta y = 0$，则有：

同理，在上面可微分等式中令$\Delta x = 0$，则有：

如果函数$f(x, y)$在点$P_0(x_0, y_0)$点可微分，那么该函数在点$P_0(x_0, y_0)$的偏导数存在，且有：

习惯上，我们把自变量的增量$\Delta x$和$\Delta y$分别记为$\textrm{d}x$和$\textrm{d}y$，这样函数的全微分为：

💡可微===>偏导数存在，但是偏导数存在不一定可微。

如果函数$z = f(x,y)$的偏导数$\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$在点$(x,y)$连续，则函数在$(x,y)$点处可微分。

✏️例子

讨论函数

在$(0, 0)$点的可微性。

⬇️ Click to expand!

按照定义可以证明: $f_x(0, 0) = f_y(0, 0) = 0$ 所以有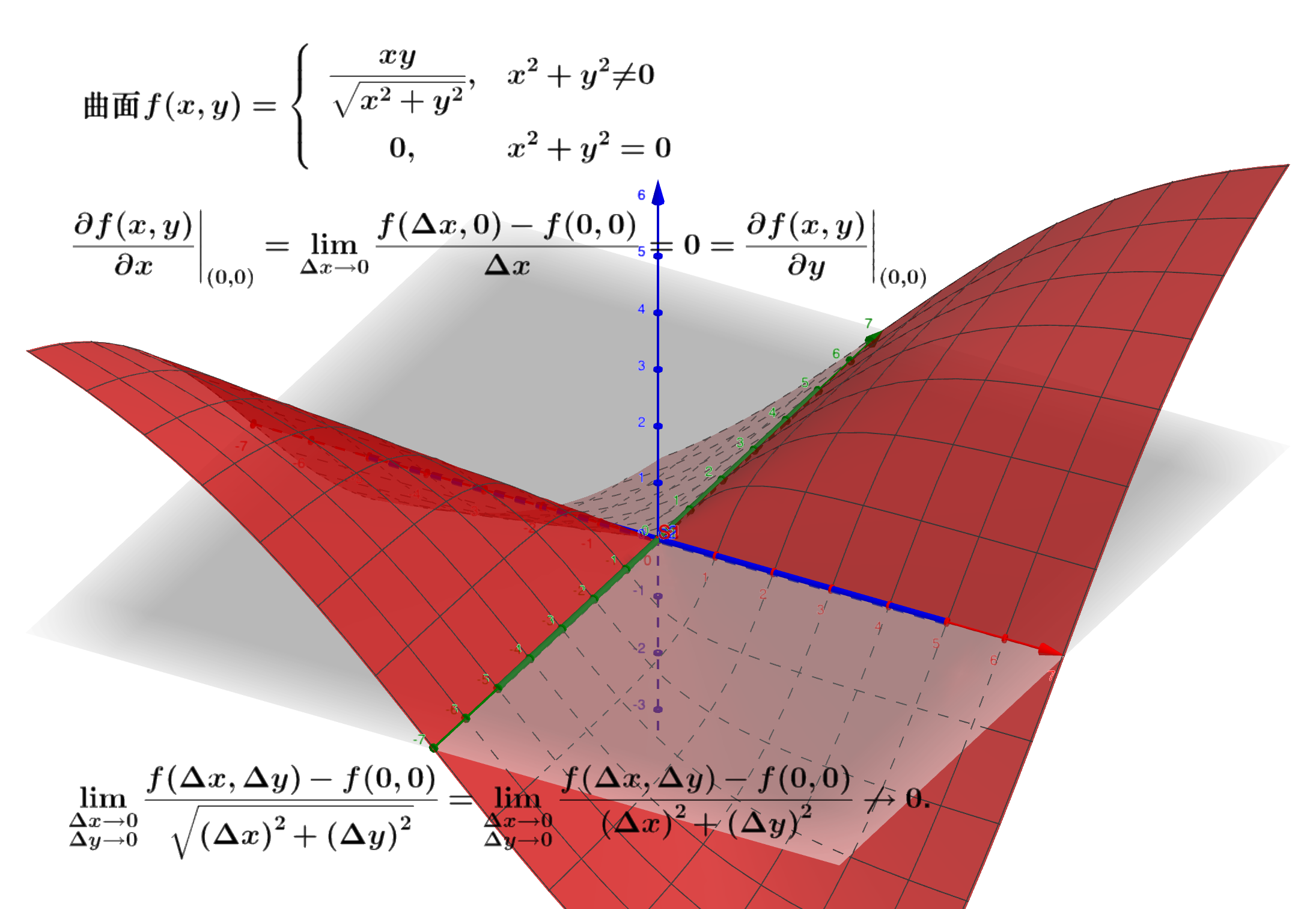， $\Delta z - \mathrm{d}z\vert_{(0, 0)}(\Delta x, \Delta y)= f(\Delta x, \Delta y) - f(0, 0)- 0\times\Delta x - 0\times\Delta y = \dfrac{\Delta x \cdot \Delta y}{\sqrt{(\Delta x)^2 + (\Delta y)^2}}$ 从而有： $\dfrac{f(\Delta x, \Delta y) - f(0, 0)- 0\Delta x - 0\Delta y}{\sqrt{(\Delta x)^2 + (\Delta y)^2}} \nrightarrow 0, (\Delta x, \Delta y) \to (0, 0)$ 所以函数在$(0, 0)$点不可微。

✏️例子 求函数$u = x - \cos \dfrac{y}{2} + \arctan \dfrac{z}{y}$的全微分。

可微的充分条件

若函数$z=f(x,y)$的偏导数在点$(x_0, y_0)$的某邻域内存在，且$f_x,f_y$在点$(x_0, y_0)$点连续，则函数$f$在点$(x_0, y_0)$点可微。

偏导数连续不是函数可微的必要条件，如函数

在$(0,0)$点可微，但是偏导函数$f_x, f_y$在$(0,0)$点不连续。

📚第四次作业:

• 求下列函数的偏导数

  • $z = \sin(xy) + \cos^2(xy)$

  • $u = x^{\dfrac{y}{z}}$

  • $u = \arctan(x - y)^z$

• 求下列函数的$\dfrac{\partial^2 z}{\partial x^2}, \dfrac{\partial^2 z}{\partial y^2}, \dfrac{\partial^2 z}{\partial x \partial y} $

  • $z = x^4 + y^4 - 4x^2y^2$

  • $z = \arctan\dfrac{y}{x}$

  • $z = y^x$

• 曲线

在点$(2, 4, 5)$处的切线对于$x$轴的倾角是多少？

• 求下列函数的全微分：

  • $z = xy + \dfrac{x}{y}$

  • $z = \dfrac{y}{\sqrt{x^2 + y^2}}$

📌5. 方向导数与梯度

偏导数研究的是二元函数沿着$x$轴方向或者$y$轴方向的变化率。我们可以更一般的讨论函数沿着任一射线方向的变化率。

以$P_0(x_0, y_0)$为起点，方向为$\mathbf{v}$的射线的参数方程为:

设$D \subset \mathbb{R}^2$为开集，$f(x,y)$为定义在$D$上的二元函数，$(x_0, y_0) \in D$，$\mathbf{v} = (\cos \alpha, \sin \alpha)$为一个方向向量，如果极限

存在，则称此极限为函数$f$在点$P_0(x_0, y_0)$点沿方向$\mathbf{v}$的方向导数，记为

曲面$z = f(x, y)$在$(x_0, y_0)$点处的方向导数如下图所示。

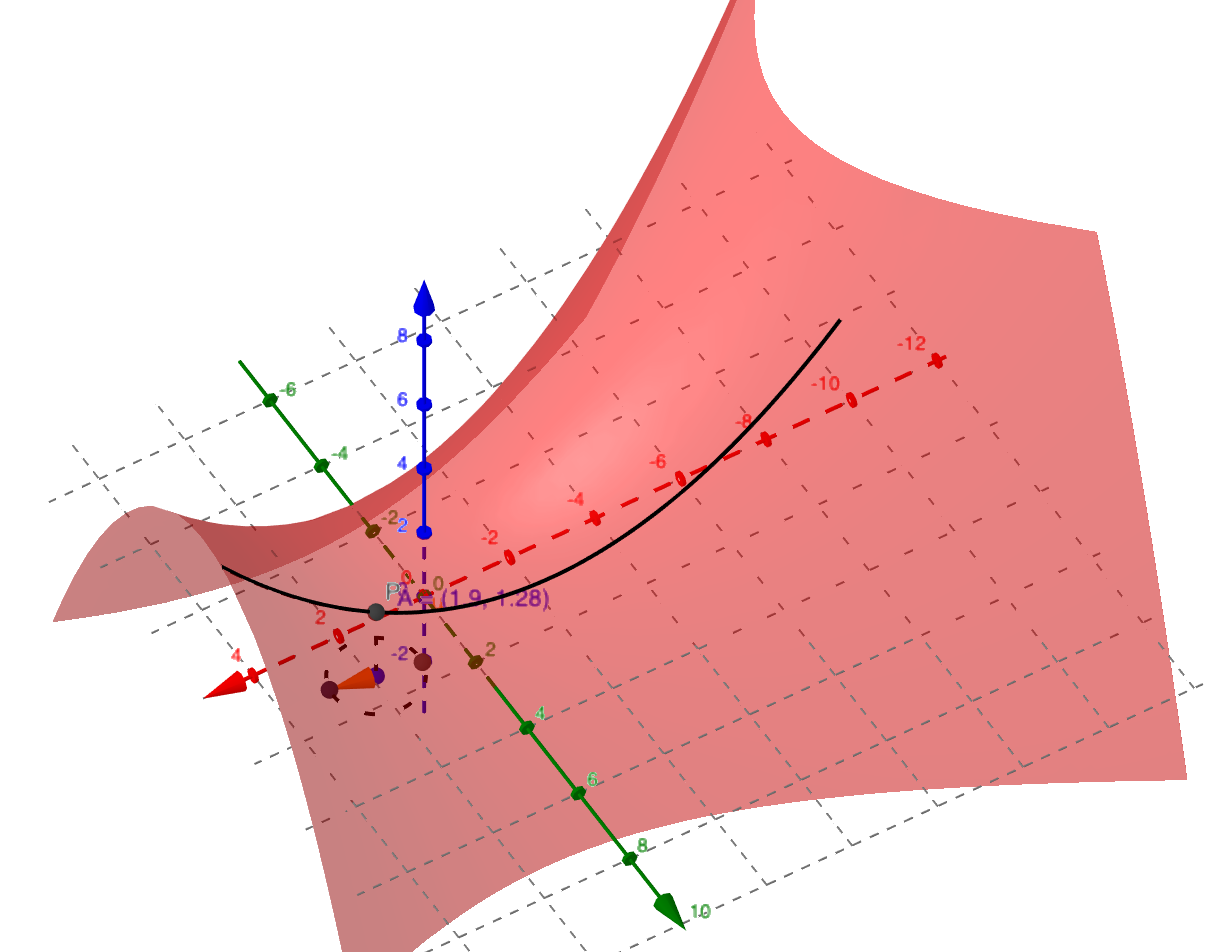
✏️例子

讨论函数$z = \sqrt{x^2 + y^2}$在$(0, 0)$点，沿着任一方向$\mathbf{v} = (\cos \alpha, \sin \alpha)$的方向导数。

解：$\left.\dfrac{\partial f}{\partial \mathbf{v}}\right\vert_{(0, 0)} = \lim\limits_{\rho \to 0+}\dfrac{f(0 + \rho \cos \alpha, 0 + \rho \sin \alpha) - f(0, 0)}{\rho} = 1$

所以函数在$(0, 0)$点沿着任一方向的方向导数为常数1，见下图：

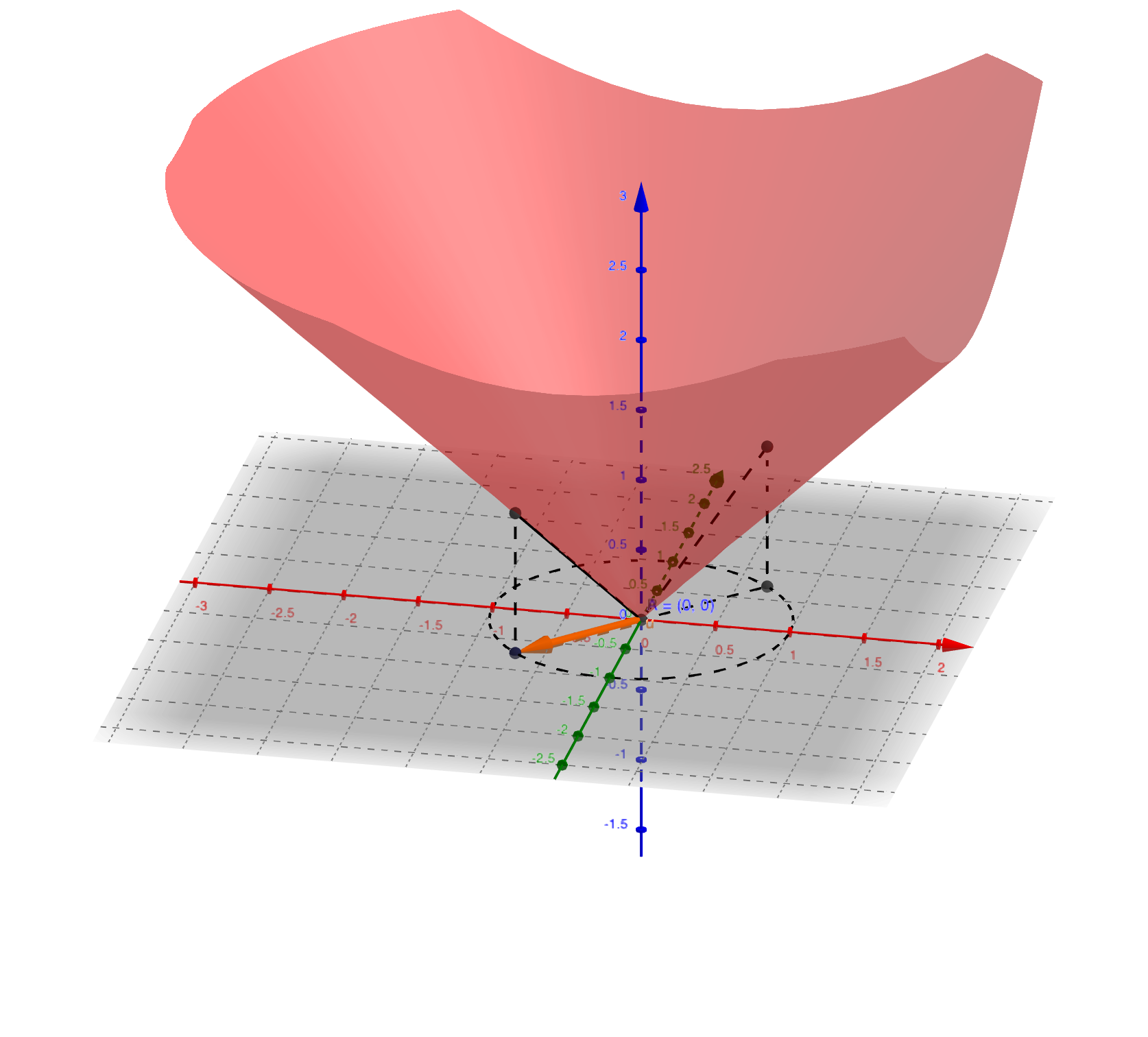
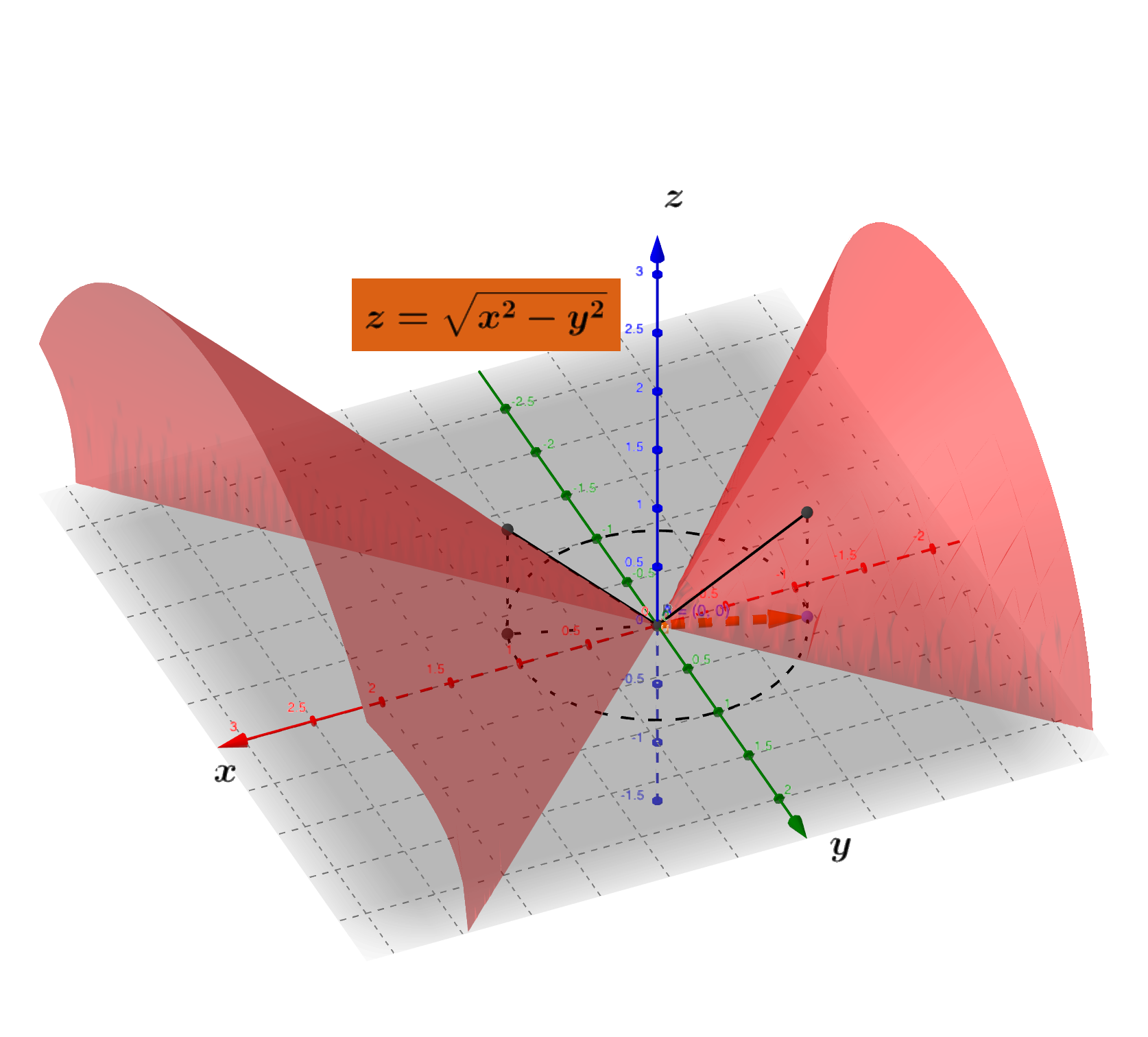
✏️例子

讨论函数$f(x, y) = \vert x^2 - y^2 \vert^{1/2}$在原点的方向导数。

解：$\dfrac{\partial f}{\partial \mathbf{v}}\vert_{(0, 0)} = \lim\limits_{\rho \to 0+}\dfrac{f(0 + \rho \cos \alpha, 0 + \rho \sin \alpha) - f(0, 0)}{\rho} = \vert \cos^2 \alpha - \sin \alpha^2 \vert^{1/2}$

• 当$\cos^2 \alpha = \sin^2 \alpha$时，沿着这样的方向，方向导数为零；

• 当$\cos^2 \alpha \ne \sin^2 \alpha$时，沿着这样的方向，方向导数为$\vert \cos^2 \alpha - \sin^2 \alpha \vert^{1/2}$；

见下图：

☘︎ 可微与方向导数的关系

设函数$f(x,y)$在$P_0(x_0, y_0)$点可微分，那么对于任一方向$\mathbf{v} = (\cos \alpha, \sin \alpha)$，$f$在$P_0(x_0, y_0)$点沿方向$\mathbf{v}$的方向导数存在，且有

☘︎ 梯度

若函数$f(x,y)$在点$P_(x_0, y_0)$对所有自变量的偏导数存在，则称向量$(f_x(x_0, y_0), f_y(x_0, y_0))$为函数在点$P_0$点处的梯度。记作：

或者

💡 “$\nabla$”读作纳布拉，称为梯度运算符。

下图为曲面:

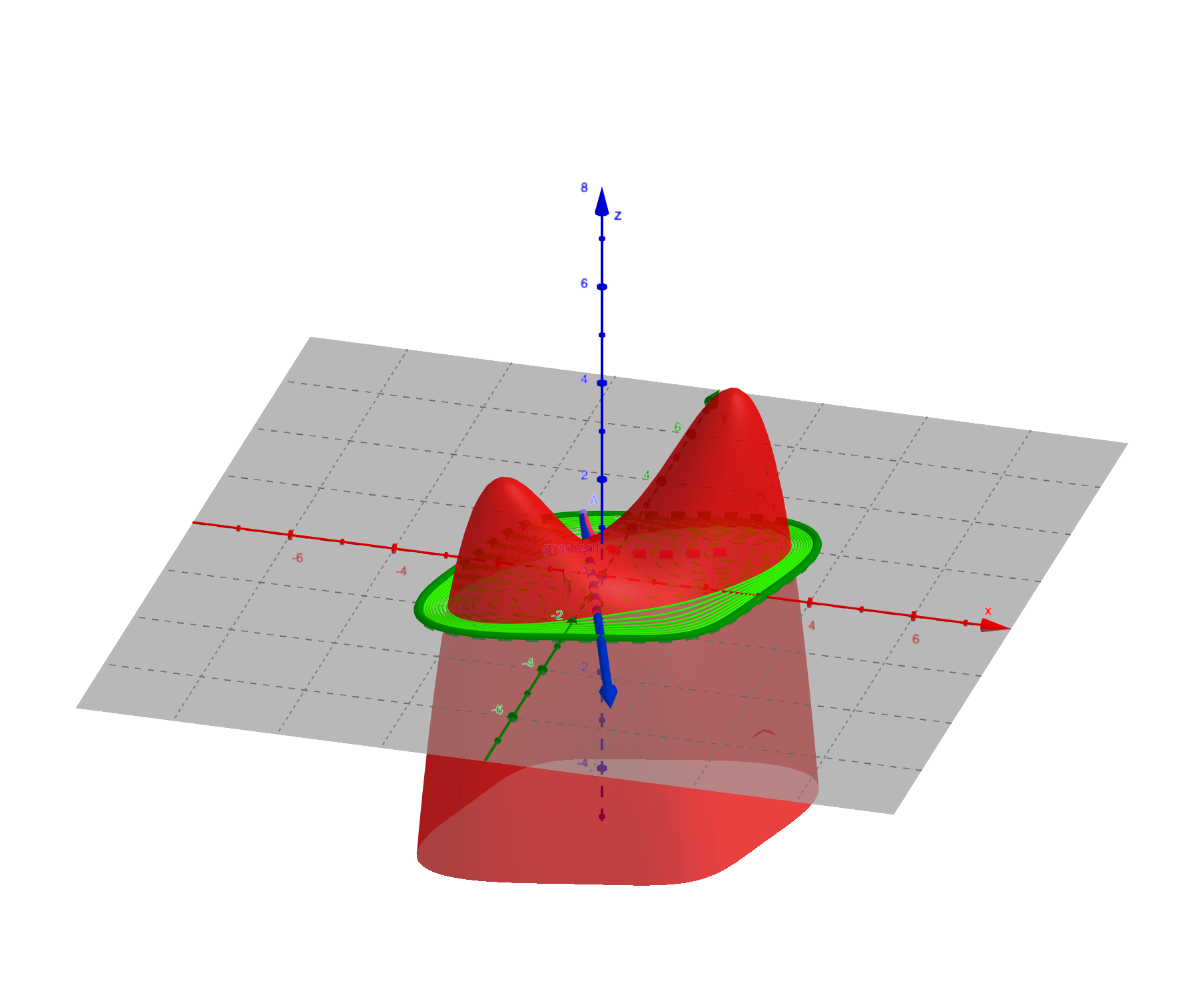
该函数在$(x, y)$处的梯度为：$(f_x(x,y), f_y(x,y)) = (\dfrac{-4x^3 + 3x^2 + 4x + 8y}{8}, \dfrac{-4y^3 + 6x + 4y - 1}{6})$.

等值线为函数的取值为常数的自变量的范围：对于二元函数来讲，: 等值线的表达式为:

下图展示了上面曲面的等值线。

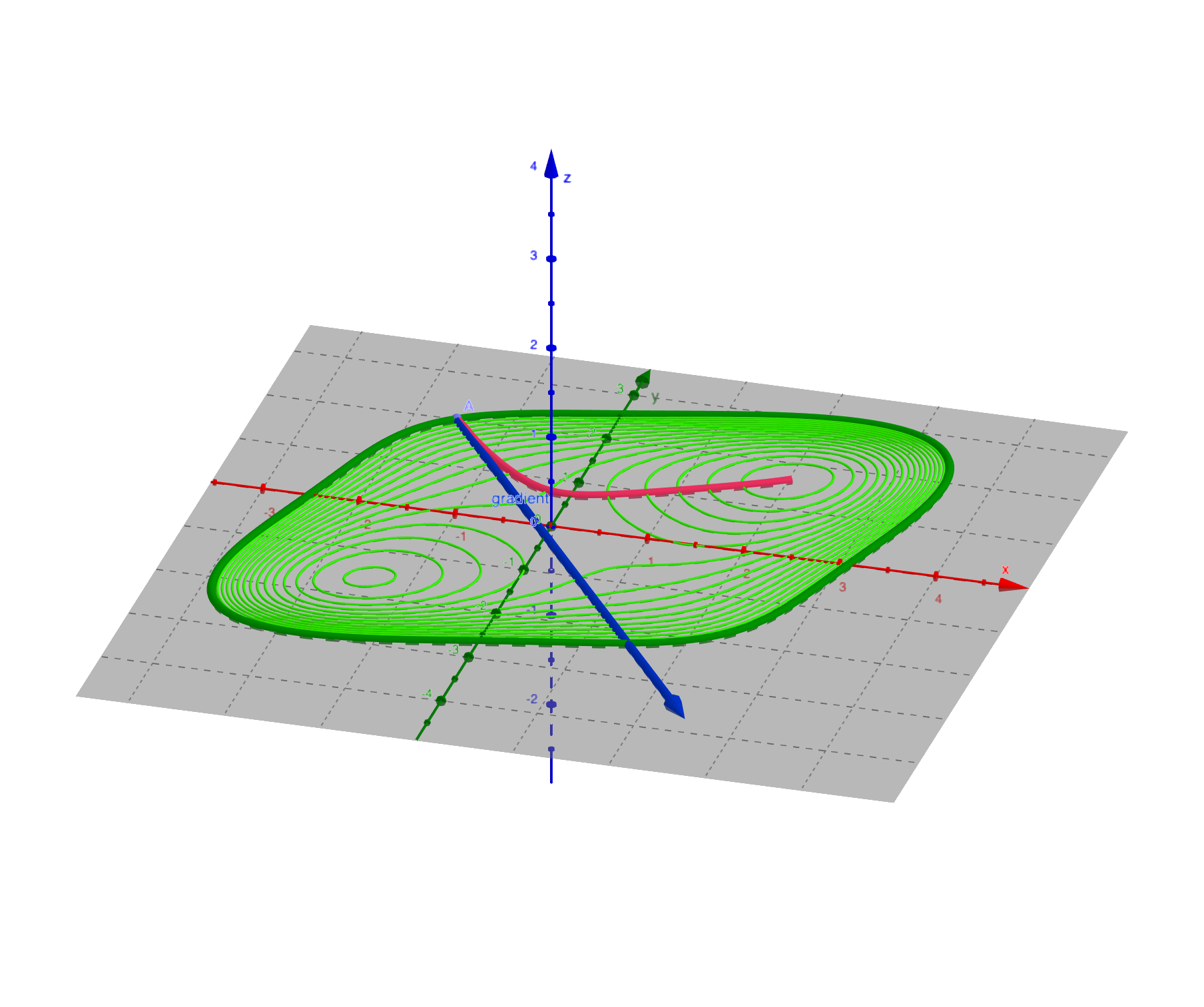
💡 从上面分析可以看出：

• 方向导数为梯度在所求方向上的投影;

• 梯度为一个向量，不是一个标量;

• 如果在一点处方向导数的方向选择为梯度方向，则方向导数最大，且值为梯度的模;

• 如果在一点处方向导数的方向选择为负梯度方向，则方向导数最小，且值为梯度的模的相反数;

• 如果在一点处方向导数的方向选择为和梯度垂直的方向，则方向导数的值为零;

• 梯度方向和等值线相互垂直，且从等值线小值指向大值.

✏️例子

设$z = x^2 - xy + y^2$，求它在$(1,1)$点的沿方向$\mathbf{v} = (\cos \alpha, \sin \alpha)$的方向导数，并指出：

• 沿着哪个方向的方向导数最大？

• 沿着哪个方向的方向导数最下？

• 沿着那个方向的方向导数为零。

⬇️ Click to expand!

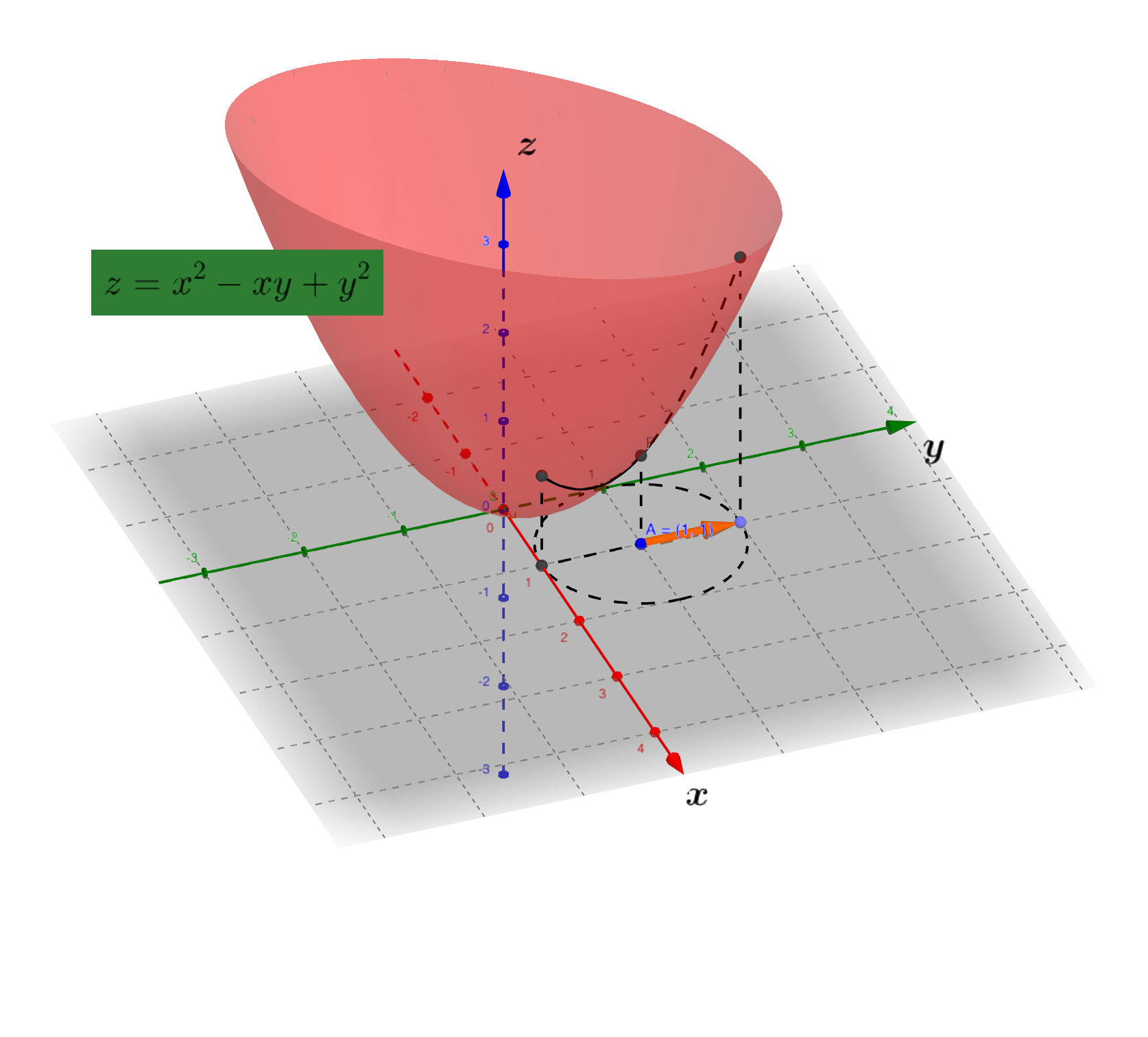
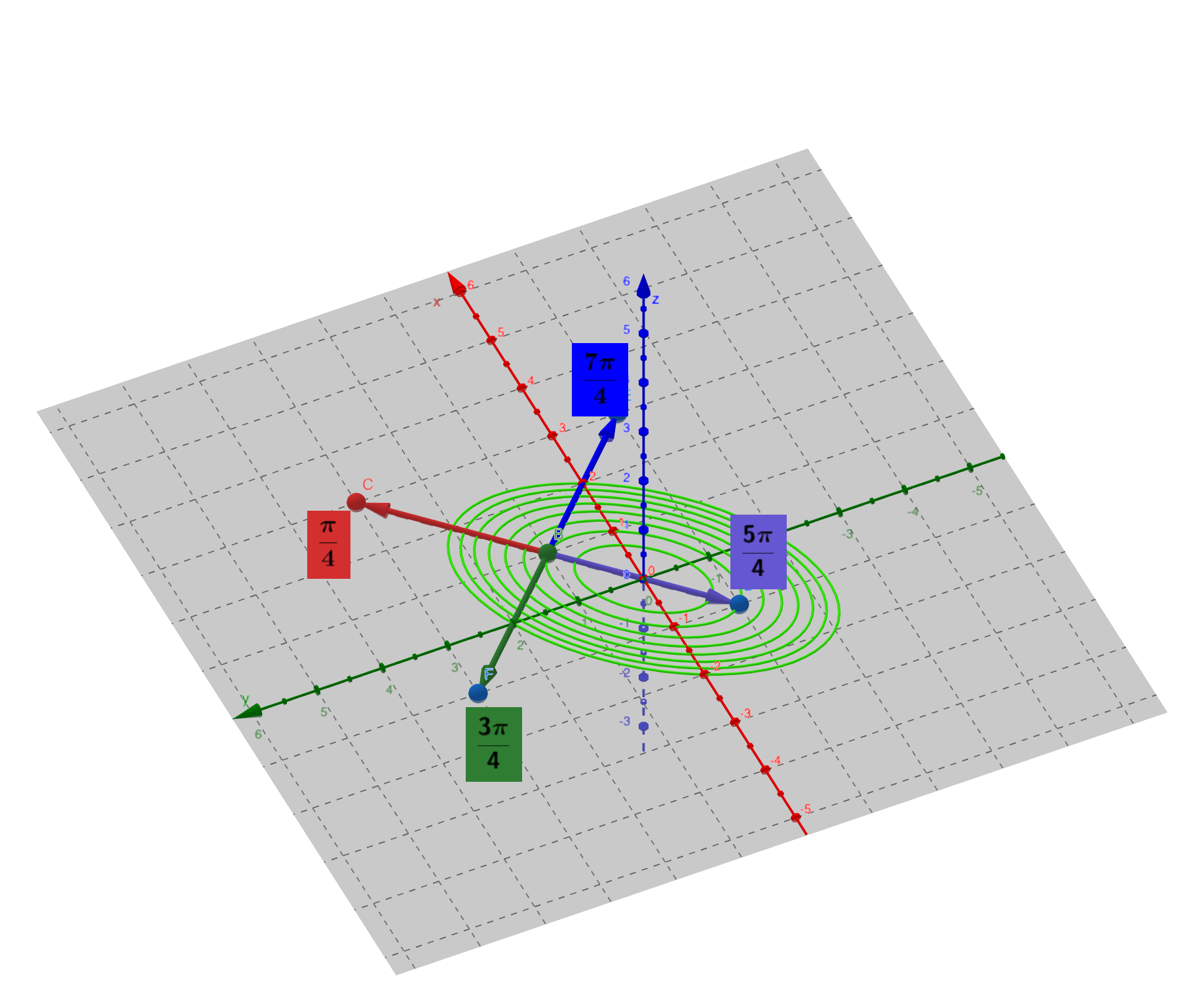
解：函数在$P_0(1,1)$处的梯度为： $\nabla f(1,1) = \left(2x - y, 2y - x\right)_{(1,1)} = (1, 1)$ 所以，函数在$(1, 1)$处沿着方向$\mathbf{v} = (\cos \alpha, \sin \alpha)$的方向导数为： $\dfrac{\partial f}{\partial \mathbf{v}}(1, 1) \cdot (\cos \alpha, \sin \alpha) = \cos \alpha + \sin \alpha = \sqrt{2}\sin (\alpha + \dfrac{\pi}{4})$ 所以，函数沿着: (1) $\alpha = \dfrac{\pi}{4}$方向导数最大，且最大值为$\Vert \nabla f(1,1) \Vert = \sqrt{2}$ (2) $\alpha = \dfrac{5\pi}{4}$方向导数最小，且最大值为$-\Vert \nabla f(1,1) \Vert = -\sqrt{2}$ (3) $\alpha = \dfrac{5\pi}{4}, \dfrac{7\pi}{4}$方向导数为零。

✏️例子

下图为马鞍面$z = x^2 - y^2$,左边为该曲面的等值线。$P$为定义域中的一点，左图蓝色射线 为等值线在$P$点处的梯度。

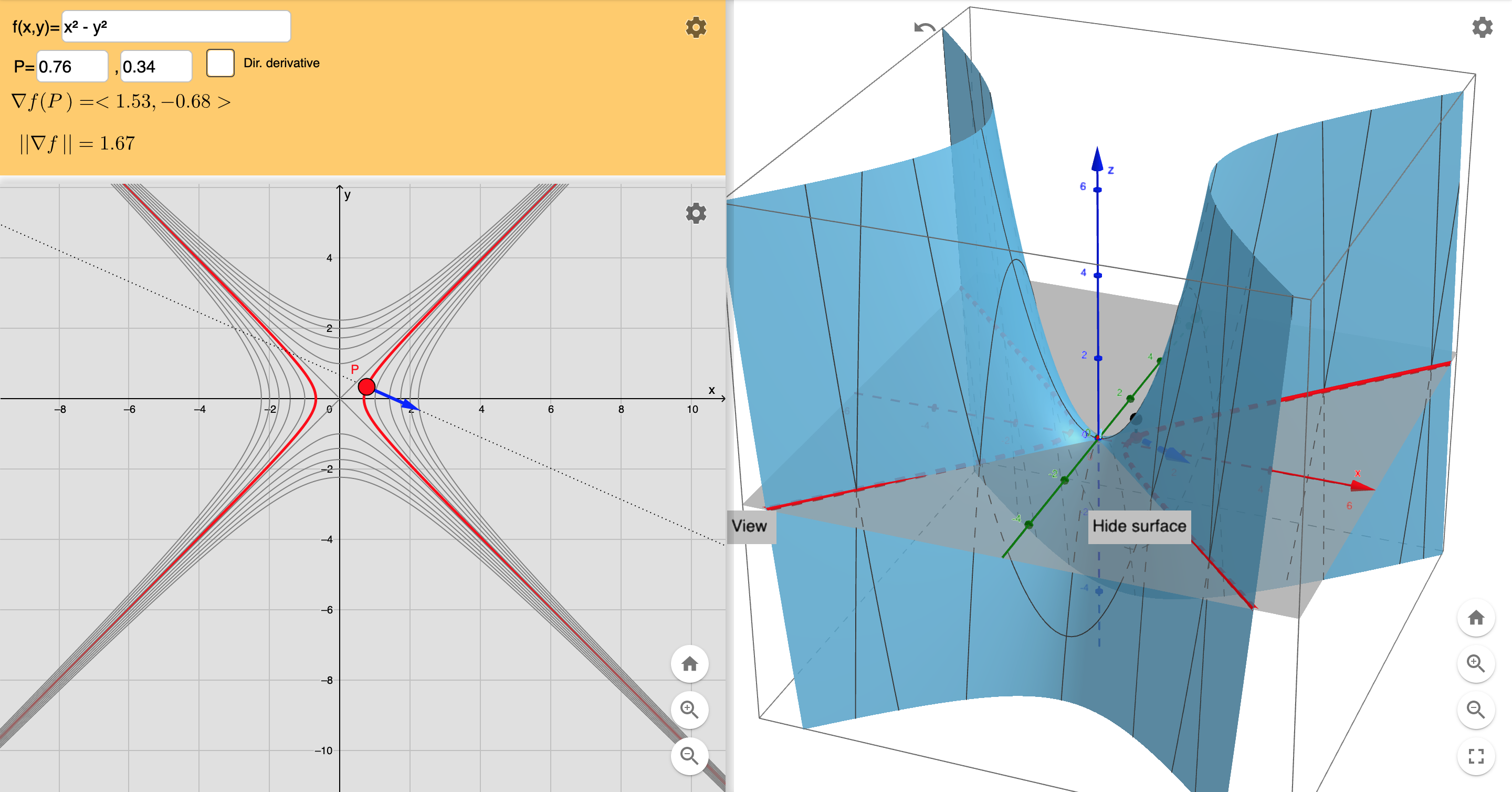
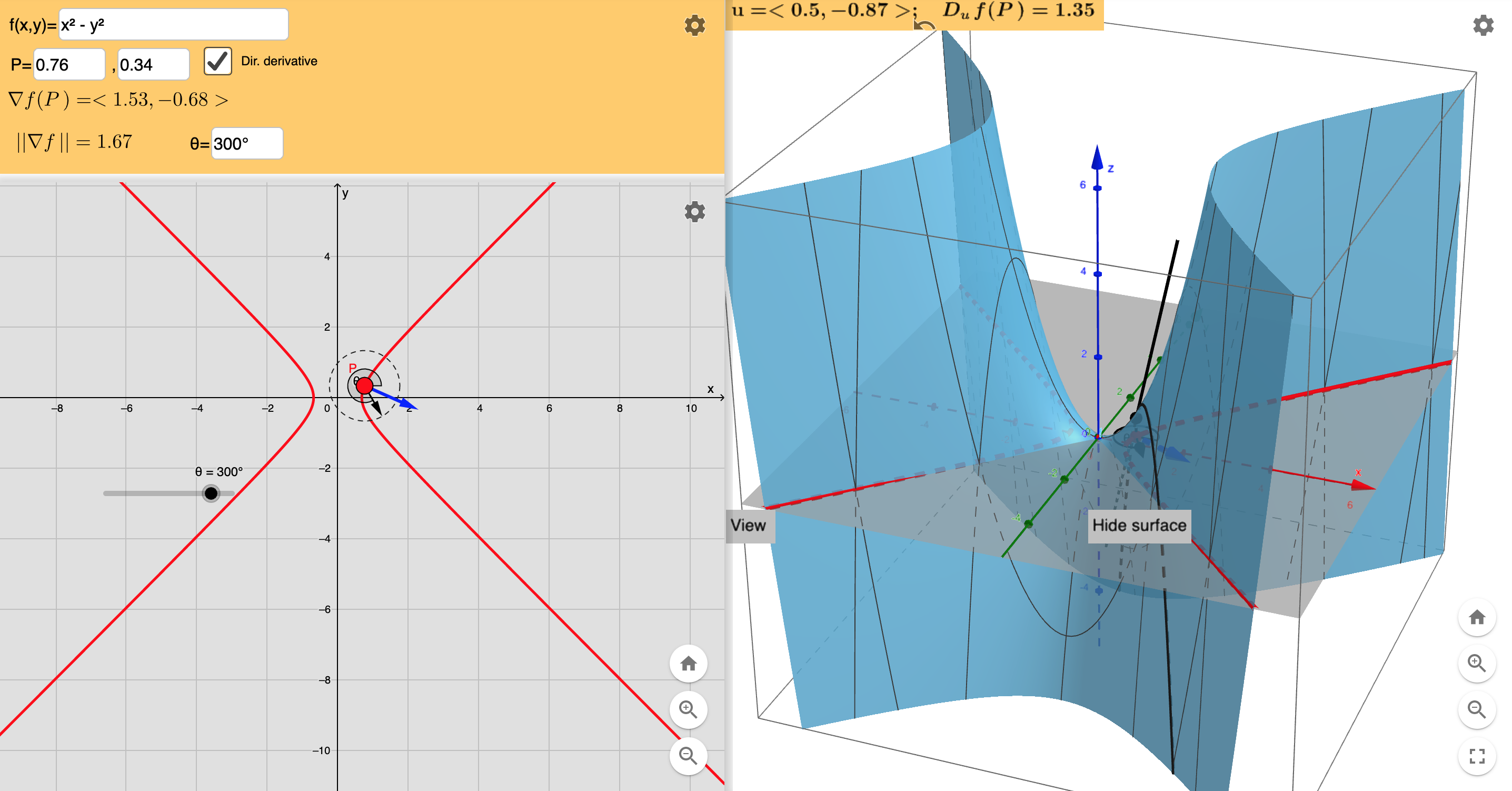
下图为方向角$\theta = 300^o$的在$P$点处的方向导数.

💡几个重要的定义：

偏导数、微分、方向导数、梯度。

• 🤔你可以写出这些概念的定义么？

• 🤔它们的几何意义是什么？

• 🤔相互逻辑关系是什么？

💡几点说明：

多元函数的导数，更一般的应该为一个矩阵(Jacobi Matrix)。例如：

• 如果$f: D \subset \mathbb{R} \to \mathbb{R}$，则$f’(x)$为一个函数(导函数);

• 如果$f: D \subset \mathbb{R}^2 \to \mathbb{R}$，则$f’(x,y) = (f_x(x,y), f_y(x,y))$;

• 如果$f: D \subset \mathbb{R}^n \to \mathbb{R}$，则$f’(x_1,x_2, \cdots, x_n) = (f_{x_1}, f_{x_2}, \cdots, f_{x_n})\vert_{(x_1, x_2, \cdots, x_n)} $;

• 如果$f: D \subset \mathbb{R}^n \to \mathbb{R}^m$，那么$f = (f_1, f_2, \cdots, f_m)^\intercal$，其中$f_i: D \to \mathbb{R}$，这时$f’(x_1, x_2, \cdots, x_n) = \left[\begin{array}{cccc} \dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} & \cdots & \dfrac{\partial f_1}{\partial x_n} \newline \dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2} & \cdots & \dfrac{\partial f_2}{\partial x_n} \newline \vdots & \vdots & \cdots & \vdots \newline \dfrac{\partial f_m}{\partial x_1} & \dfrac{\partial f_m}{\partial x_2} & \cdots & \dfrac{\partial f_m}{\partial x_n}\end{array} \right]$.

📚第五次作业:

• 求函数$z = x^2 + y^2$在点$(1,2)$处沿着从点$(1,2)$到点$(2, 2+\sqrt{3})$的方向的方向导数。

• 求函数$z = 1 - \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2}$在点$(\dfrac{a}{\sqrt{2}}, \dfrac{b}{\sqrt{2}})$c处沿曲线$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$在这点的内法线方向的方向导数。

• 设$f(x,y,z) = x^2 + 2y^2 + 3z^2 + xy + 3x - 2y - 6z$，求$\nabla f(0, 0, 0), \nabla f(1, 1, 1)$

📌6. 复合函数求导法则

⛓链式规则(chain rule)

设$z = f(x,y): D_f \subset \mathbb{R}^2 \to \mathbb{R}$，而$g: D_g \subset \mathbb{R}^2 \to \mathbb{R}^2$，如果$g(D_g) \subset D_f$，那么可以构成符合函数：

这里$g$表示为：$(u, v) \to (x(u, v), y(u, v))$.

设$g$在$(u_0, v_0) \in D_g$点可导，即$x = x(u, v), y = y(u, v)$在$(u_0, v_0)$点可偏导。记$x_0 = x(u_0, v_0), y_0 = y(u_0, v_0)$，如果$f$在$(x_0, y_0)$点可微，则有：

采用矩阵的写法为：

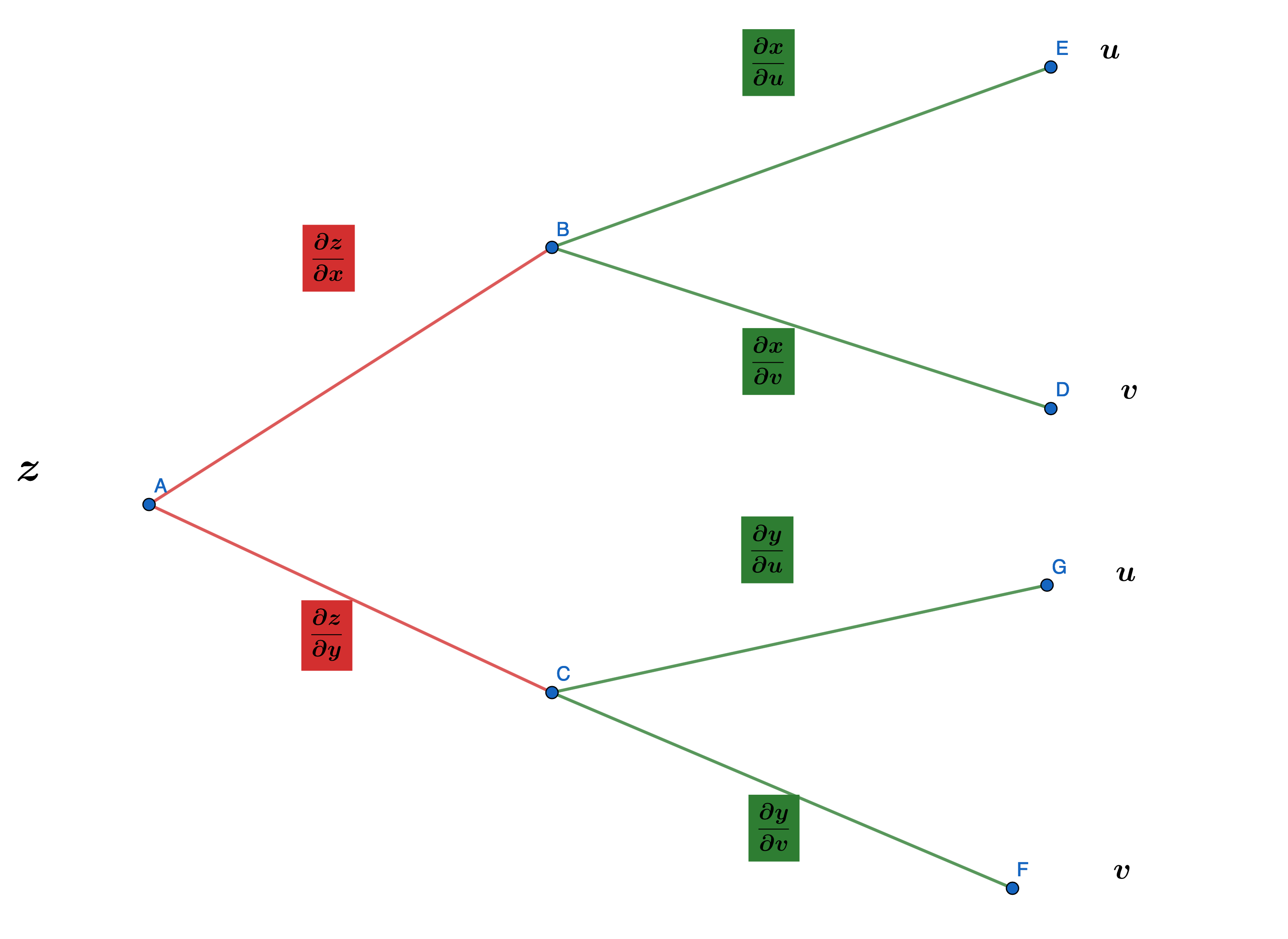
✏️例子

设$z = ax + by, x = cu + dv, y = eu + fv (a, b, c, d \in \mathbb{R})$，求$\dfrac{\partial z}{\partial u}, \dfrac{\partial z}{\partial v}$

🤔思考

• 两个线形变换复合函数的导数对应于导数的乘积

• 两个非线形变换复合函数的导数对应于❓❓的❓❓

✏️例子

设$z = \dfrac{x^2}{y}, x = u - 2v, y = 2u + v $，求$\dfrac{\partial z}{\partial u}, \dfrac{\partial z}{\partial v}$

✏️例子

设$w = f(x^2 + y^2 + z^2, xyz) $，$f$具有连续的二阶偏导数，求$\dfrac{\partial f}{\partial x}, \dfrac{\partial^2 f}{\partial x \partial z}$

✏️例子

设$z = f(u, v, t) = uv + \sin t$，而$u = e^t, u = \cos t$，求导数$\dfrac{\mathrm{d}z}{\mathrm{d}t}$

📚第六次作业:

• 设$z = u^2 + v^2, u = x + y, v = x - y$，求$\dfrac{\partial z}{\partial x}, \dfrac{\partial z}{\partial y}$.

• 求函数$u = f(x^2 - y^2, e^{xy})$的一阶偏导数.

• 设$z = f(xy^2, x^2y)$求$\dfrac{\partial^2 z}{\partial x^2}, \dfrac{\partial^2 z}{\partial x \partial y},\dfrac{\partial^2 z}{\partial y^2} $

📌7. 隐函数求导法则

☘︎ 隐式函数

之前我们接触的函数，其表达式大多是自变量的某个算式，如：

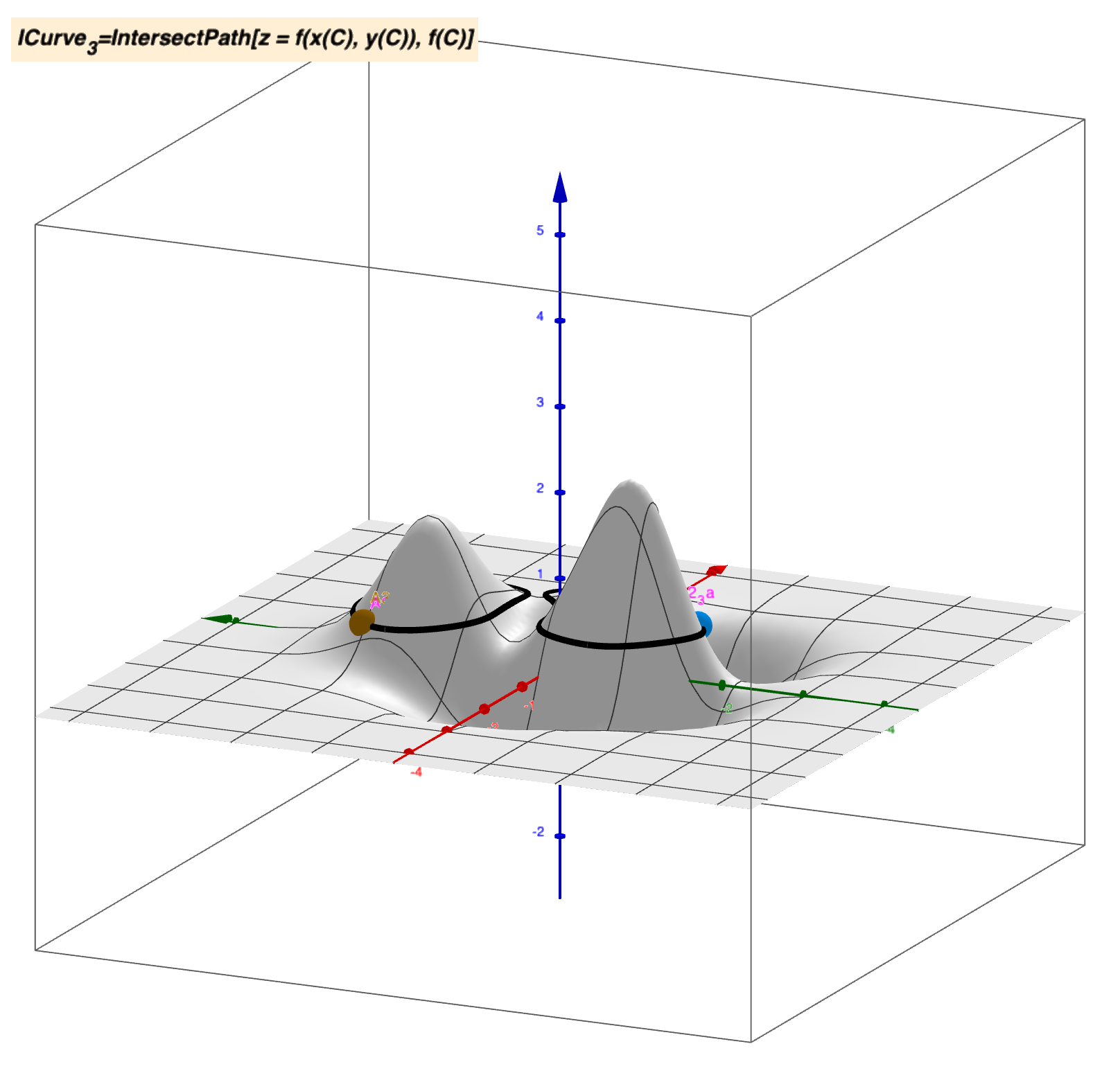
这种形式的函数称为显函数。但是在不少情况下常常会遇到另一种形式的函数，其自变量与因变量之间的对应法则有一个方程所确定，通常称为隐函数。例如：$z = x^2 + y^2$这个二元函数，当确定$z = 1$时，确定了一个隐函数：$x^2 + y^2 = 1$。例如曲面

当$z = 0.44$时得到方程，见下图：

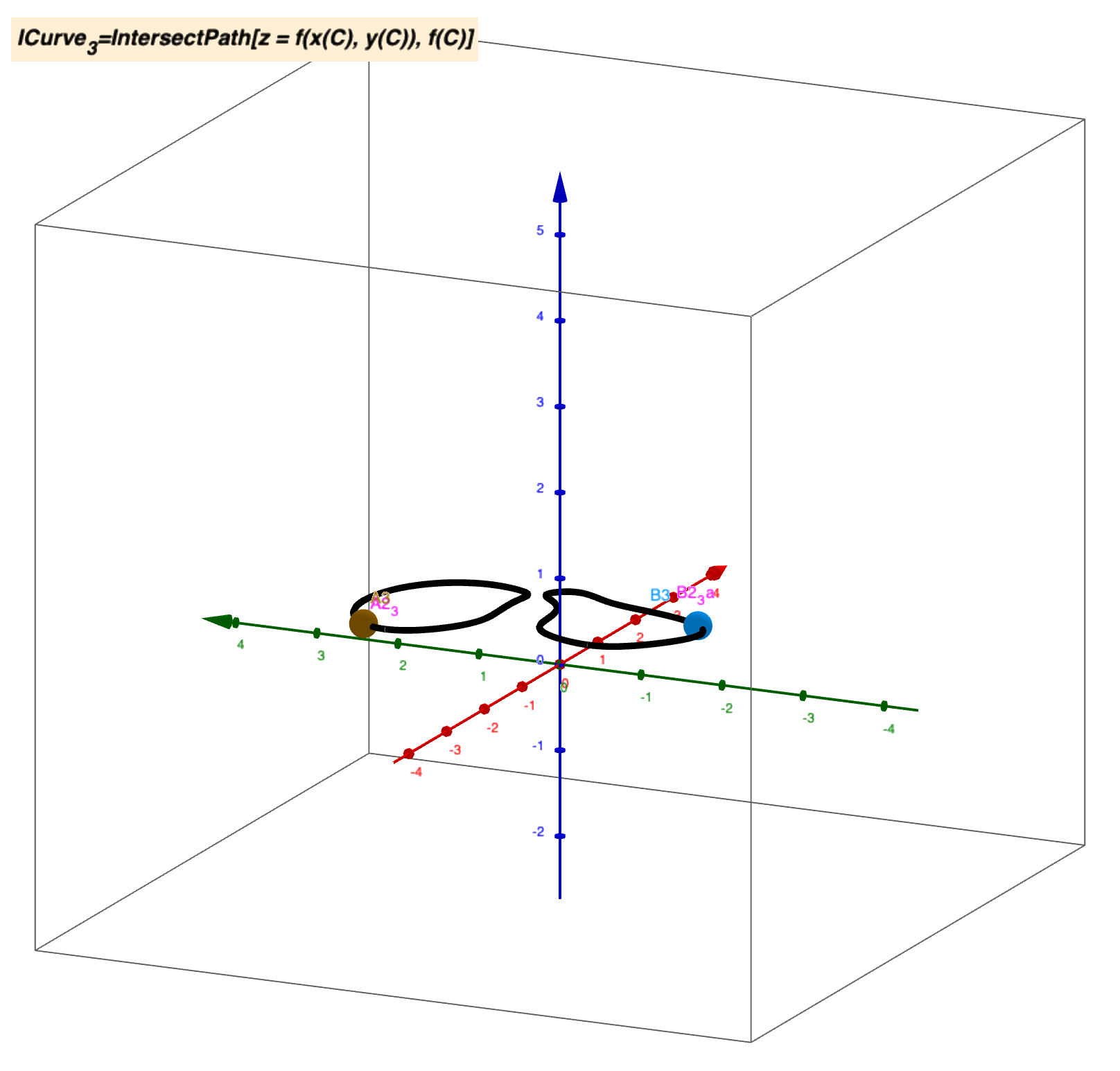
☘︎ 隐式方程定理

设函数$F(x,y)$在点$P_0(x_0, y_0)$的某一邻域内具有连续的偏导数，且满足：

• $F(x_0, y_0) = 0$(初始条件)；

• $F_y(x_0, y_0) \ne $(偏导数不为零)；

则方程$F(x, y) = 0$在点$P_0(x_0, y_0)$的某一邻域内能唯一确定✅一个连续且具有连续导数的函数$y = f(x)$，它满足：

• $y_0 = f(x_0)$;

• $\dfrac{\mathrm{d}f}{\mathrm{d}x} = \dfrac{-F_x}{F_y}$(求导公式)

✏️例子

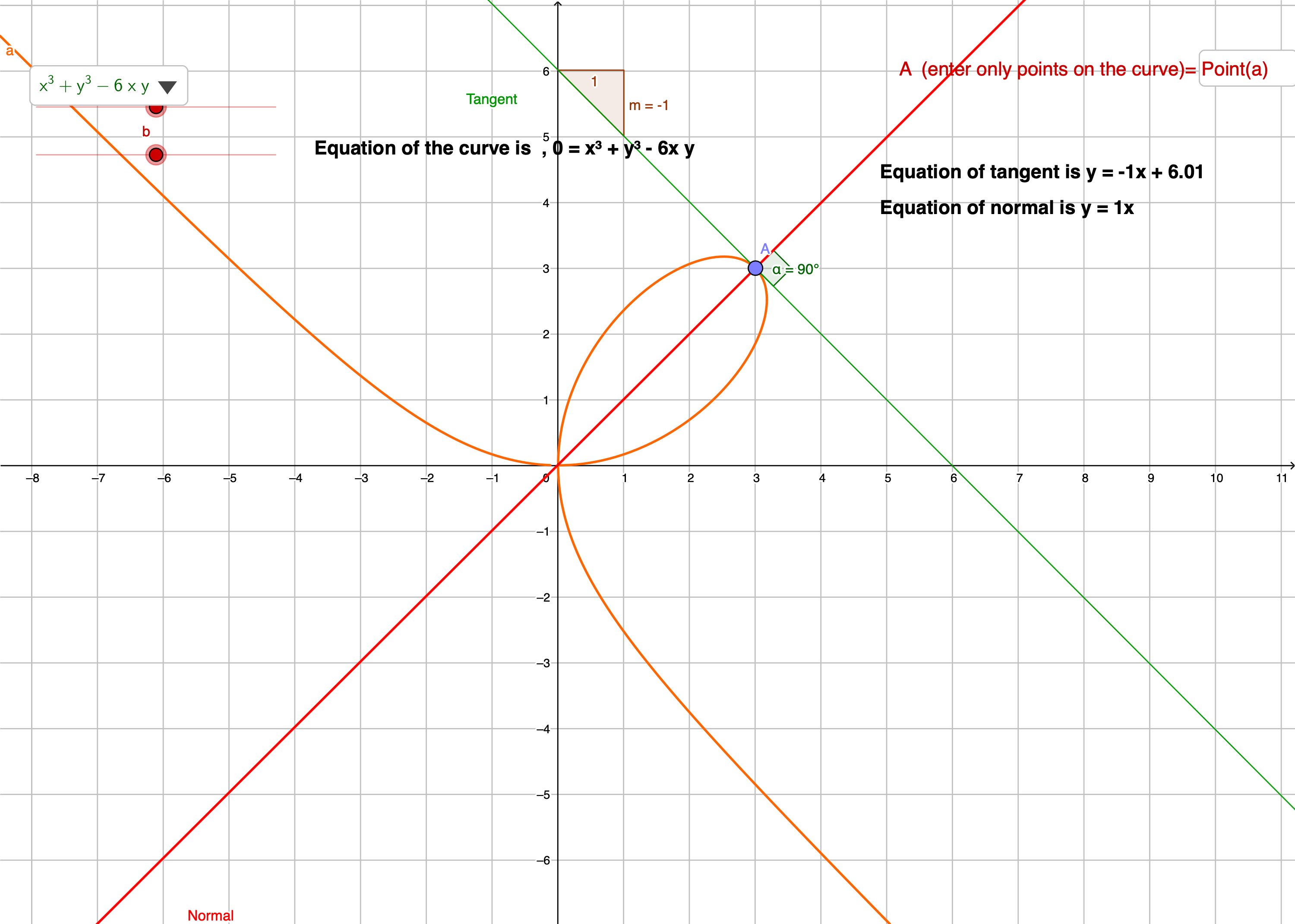
笛卡尔叶形线(folium of Descartes)首先由笛卡尔在1638年提出。笛卡尔叶形线的隐式方程为：

该曲线在第一象限形成一个闭合曲线，且渐近线为$y = x$，关于$y = x$对称。

该曲线由笛卡尔在1638年提出，针对费马声称有一种方法能够找到曲线的切线和法线方程。笛卡尔提出该曲线让费马去寻找在任意一点的切线和发现方程（笛卡尔办不到啊）。其结果是：费马利用隐函数求导法则很容易找到了该曲线的切线和法线方程。

下面我们来求解该曲线$x^3 + y^3 - 6xy = 0$的在$(3, 3)$点的切线和法线方程。

解：

首先可以验证该曲线在$(3,3)$点附近确定了一个函数$y = f(x)$，因为若令$F(x,y) = x^3 + y^3 - 6xy$.可以验证$F(3,3) = 0, F_y(3,3) = (3y^2 - 6x)_{(3,3)} = 9 \ne 0$.

斜率：$k = -\dfrac{F_x}{F_y}(3,3) = -\dfrac{3x^2 - 6y}{3y^2 - 6x} = -1$

或者对于方程的两边关于$x$求导数得到：

得到$k = -1$

所以：

• 切线方程为： $y - 3 = -(x - 3)$;

• 法线方程为： $y - 3 = (x - 3)$.

上式关于$x$继续求导数，得到；

从上式中可得到$\dfrac{\mathrm{d}^2y}{\mathrm{d}x^2}$

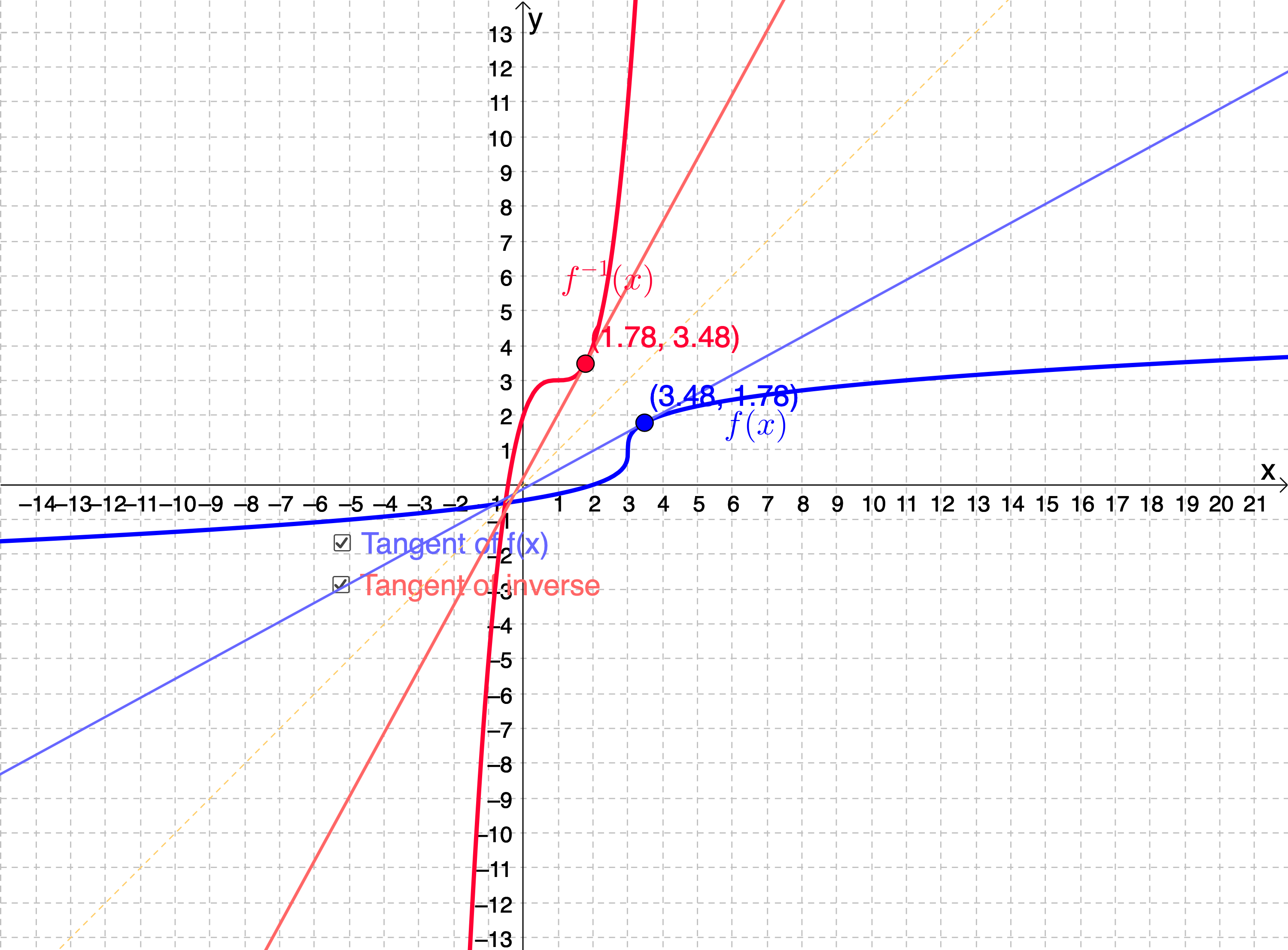
✏️例子(反函数求导公式)

设$y = f(x)$在$x_0$的某邻域上具有连续的导数$f’(x)$，且$f(x_0) = y_0$，考虑方程

由于

所以只要$f’(x_0) \ne 0$得到隐函数$x = g(y)$为$y = f(x)$的反函数。且有：

☘︎ 隐式方程组

设有方程组

其中$F(x, y, u, v), G(x, y, u, v)$为定义在$D \subset \mathbb{R}^4$上的4元函数。若存在平面区域$E, F \subset \mathbb{R}^2$，对于$E$中的每一个点$(x, y)$，有唯一的$(u, v) \in F$，使得$(x, y, u, v) \in D$，且满足上方程组，则称有方程组确定了✅隐式方程组

并在$D$上成立恒等式

☘︎ 隐式方程组定理

若

• $F(x, y, u, v)$与$G(x, y, u, v)$在以$P_0(x_0, y_0, u_0, v_0)$为内点的区域$D \subset \mathbb{R}^4$上连续；

• $F(x_0, y_0, u_0, v_0) = 0, G(x_0, y_0, u_0, v_0) = 0$(初始条件)；

• 在$D$上$F, G$具有连续的一阶偏导数；

• $J = \dfrac{\partial (F, G)}{\partial (u, v)} = \left\vert\begin{array}{cc} F_u & F_v \newline G_u & G_v \end{array}\right\vert_{P_0} \ne 0$

则：

• 在点$P_0$的某一邻域内方程组确定了定义在$Q_0(x_0, y_0)$的某一(二维空间)邻域$U(Q_0)$的两个二元隐函数$u = f(x, y), v = g(x, y)$，使得

  • $(x, y, f(x,y), g(x,y)) \in U(P_0)$;

  • $F(x, y, f(x,y), g(x,y)) \equiv 0$

  • $G(x, y, f(x,y), g(x,y)) \equiv 0$

• $f(x,y), g(x,y)$在$U(Q_0)$上连续；

• $f(x,y), g(x,y)$在$U(Q_0)$上具有连续偏导数，且有

✏️例子

讨论方程组

在$P_0(2,1,1,2)$近旁确定怎样的隐函数组，并求其偏导数。

😓😓😓 A lot of math!

☘︎ 反函数组与坐标变换

设函数组

确定了一个从二维空间到二维空间的变换，把该方程组改写为：

如果在$P_0(x_0, y_0)$点满足：

则在$P’_0(u_0, v_0)$的某一邻域内$U(P’_0)$上存在唯一的反函数组

使得$x_0 = x(u_0, v_0), y_0 = y(u_0, v_0)$

此外，反函数方程组存在连续的一阶偏导数，且有：

另有：

😓😓😓 A lot of math!

✏️例子

平面上的点$P$的直角坐标$(x, y)$与极坐标$(\rho, \theta)$之间的坐标变换公式为：

由于

所以除原点外，方程组存在反变换方程组：

📚第七次作业:

• 设$\ln \sqrt{x^2 + y^2} = \arctan\dfrac{y}{x}$，求$\dfrac{\mathrm{d}y}{\mathrm{d}x}$

• 设$x + 2y +z - 2\sqrt{xyz} = 0$，求$\dfrac{\partial z}{\partial x}, \dfrac{\partial^2 z}{\partial x \partial y}$

• 设

  $\left\{\begin{array}{l} x = e^u + u\sin v \newline y = e^u - u\cos v \end{array}\right.$

  求$\dfrac{\partial u}{\partial x}, \dfrac{\partial u}{\partial y}, \dfrac{\partial v}{\partial x}, \dfrac{\partial u}{\partial y}$

📌8. 多元函数微分几何应用

☘︎ 空间曲线的切线与法平面

☘︎ 首先设平面曲线由方程$F(x,y) = 0$给出，它在$P_0(x_0, y_0)$点的某个邻域内满足隐函数存在条件，于是在$P_0$点附近确定一个连续可微函数$y = f(x)$(或者$x = g(y)$),其切线和法线方程为：

由于$f’(x) = -\dfrac{F_x}{F_y}$ 所以曲线$F(x,y) = 0$ 在$P_0(x_0, y_0)$点的切线和法线方程为：

☘︎ 下面讨论曲线由参数方程$x = x(t), y = y(t), z = z(t), \alpha \le t \le \beta$表示的空间曲线在$P_0(x_0, y_0, z_0)$点的切线和法平面方程，这里$x_0 = x(t_0), y_0 = y(t_0), z_0 = z(t_0)$.

我们知道空间曲线在一点的切线可以看作割线的极限，对于上述参数方程假设：

在曲线上$P_0(x_0, y_0, z_0)$点的附近选取一点$P(x, y, z)$，于是连接$P_0P$的割线方程为：

上式同除以$\Delta t$得到：

当$\Delta t \to 0$,得到在$P_0$点的切线方程为：

在$P_0$点的法平面方程为：

☘︎ 当空间曲线由方程

给出。若它在$P_0(x_0, y_0, z_0)$点的某邻域上满足隐函数存在的条件。这里不妨假设$\left.\dfrac{\partial (F, G)}{\partial (x, y)}\right\vert_{P_0} \ne 0$。则方程在$P_0$点附近能唯一确定连续可微隐函数组

且

在$P_0$点附近，得到空间曲线的参数方程为：

所以切线方程为：

即，整理后的切线方程

整理后的法平面方程

空间曲线的切向量为：

曲线

在$P_0$点的法平面就是由梯度向量$\mathbf{Grad}F(P_0), \mathbf{Grad}G(P_0)$张成的过$P_0$点的平面.

✏️例子

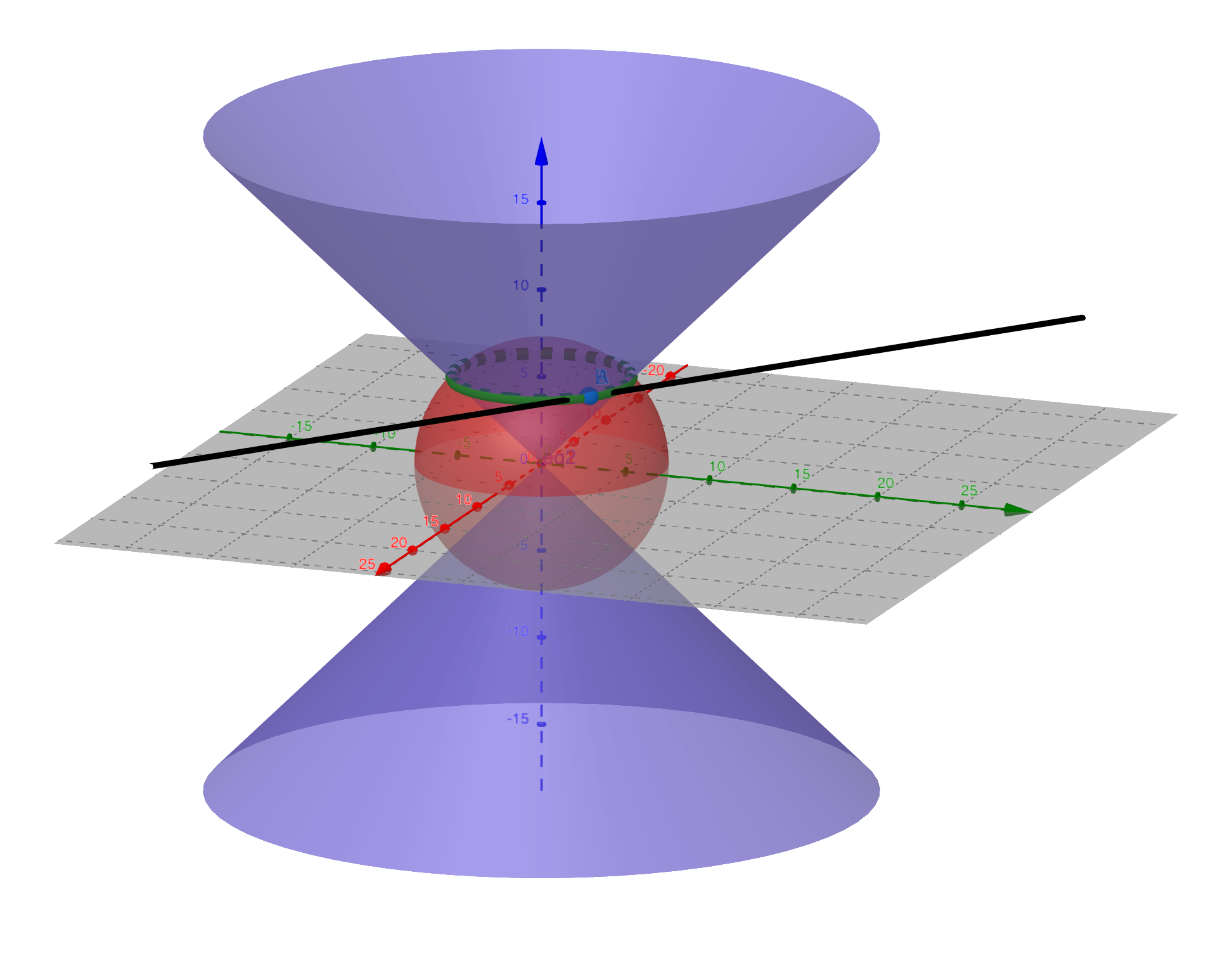
求球面$x^2 + y^2 + z^2 = 50$与锥面$x^2 + y^2 = z^2$所截出的曲线在$(3,4,5)$的切线和法平面方程。

解： 令$F(x, y, z) = x^2 + y^2 + z^2 -50, G(x, y, z) = x^2 + y^2 - z^2$，则有曲线在该点的切向量为：

所以法平面方程为：

切线方程为：

空间曲面的切平面与法向量

☘︎ 设曲面$S$方程的一般表示为：

这里考虑$F$具有连续的偏导数，且$F_x^2 + F_y^2 + F_z^2 \ne 0$，$P_0(x_0, y_0, z_0)$为曲面$S$上的一点。考察曲面$S$上过点$P_0$ 的任意一条光滑曲线$\Gamma$:

并设$x_0 = x(t_0), y_0 = y(t_0), z_0 = z(t_0)$，由于$\Gamma$在曲面$S$上，所以有：

对$t$在$t_0$处求导得到：

这说明，曲面$S$上过$P_0$的任意一条光滑曲线$\Gamma$在$P_0$点的切线都与向量：

垂直，因此这些切线都在一张平面$\Pi$上。平面$\Pi$称为曲面$S$在$P_0$点的切平面,它的法向量$\mathbf{n}$为曲面$S$在$P_0$点的法向量。

空间曲面$S$在$P_0$点处的切平面方程为：

空间曲面$S$在$P_0$点处的法向量为：

☘︎ 若空间曲面由方程$z = f(x,y)$给出，也就是$F(x, y, z) = z - f(x, y) = 0$，则曲面在$P_0(x_0, y_0, z_0)$点处的法向量为：

所以曲面$z = f(x, y)$在$P_0(x_0, y_0, z_0)$点处的切平面和法向量为：

☘︎ 强调一点

空间曲面$z = f(x,y)$在$P_0(x_0, y_0, z_0$点的切平面方程为：

所以在该切平面上(注意是切平面，不是曲面)：

• 曲面$z = f(x,y)$在$P_0$点的全微分$\mathrm{d}f\vert_{P_0}(\Delta x, \Delta y)$表示切平面从$(x_0, y_0)$到$(x_0 + \Delta x, y_0 + \Delta y)$的增量；

• $f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0)$表示曲面的增量。

见下图：

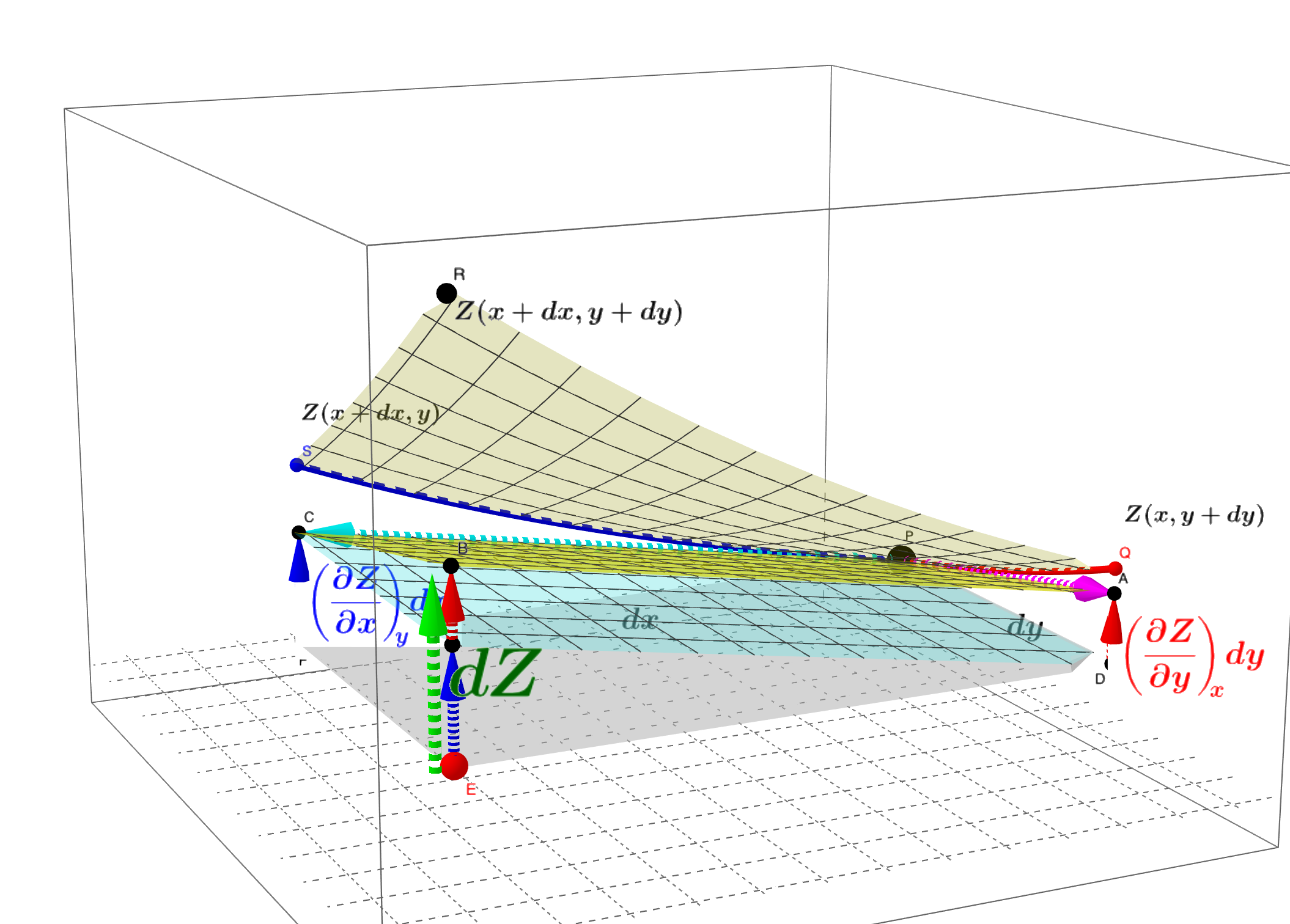
✏️例子

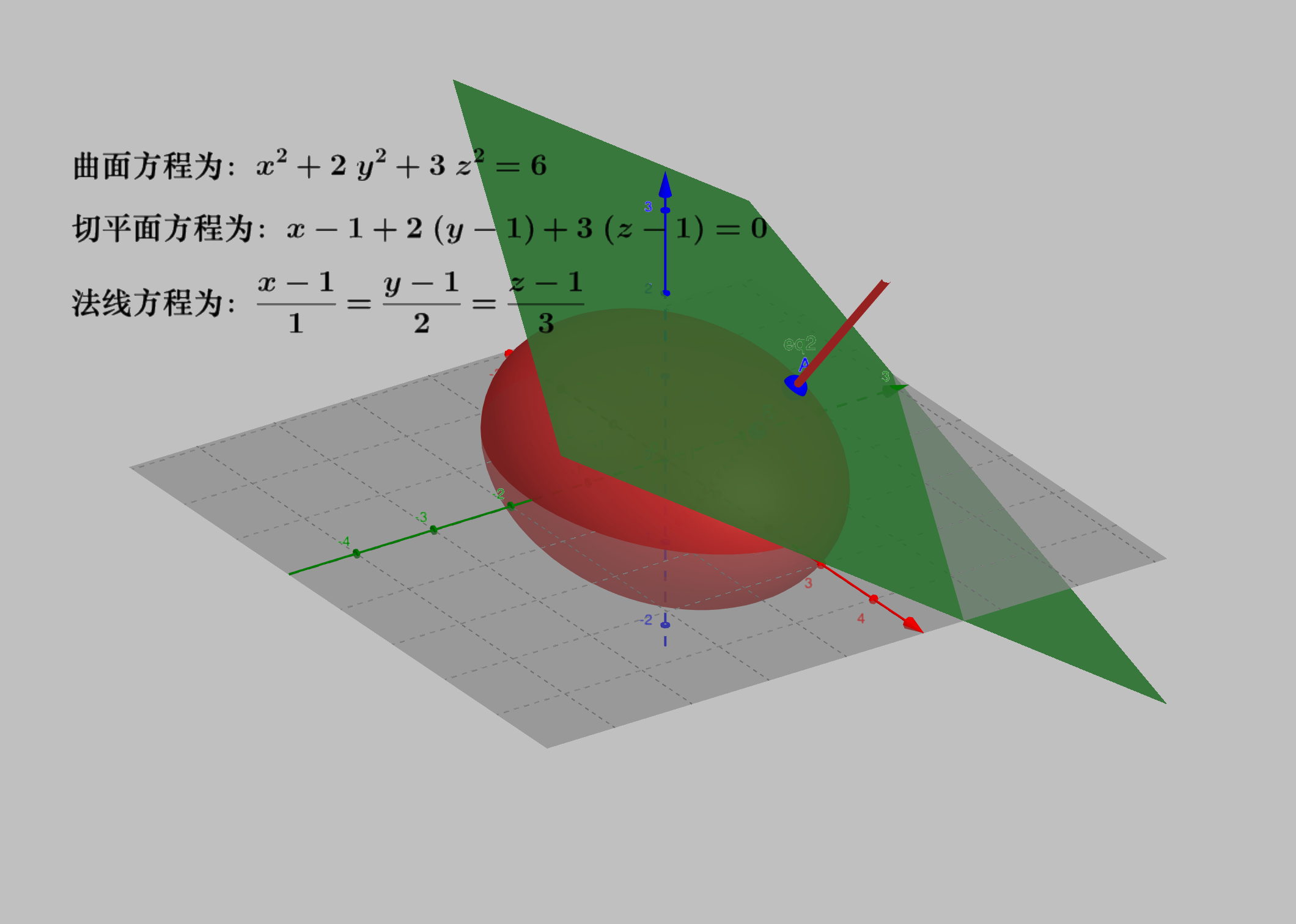
求椭球面$x^2 + 2y^2 + 3z^2 = 6$在(1,1,1)处的切平面方程和法线方程。

解： 令$F(x,y,z) = x^2 + 2y^2 + 3z^2 - 6$，则曲面在$(1,1,1)$点处的法向量为$\pm(1, 2, 3)$.所以该曲面在$(1,1,1)$点处的切平面和法线方程分别为：

📚第八次作业:

• 求曲线$\mathbf{r}(t) = (t - \sin t)\mathbf{i} + (1 - \cos t)\mathbf{j} + (4 \sin \dfrac{t}{2})\mathbf{k}$在$t_0 = \dfrac{\pi}{2}$相应点处的切线和法平面方程。

• 求曲线 $\left\{\begin{array}{l} x^2 + y^2 + z^2 - 3x = 0 \newline 2x - 3y + 5z - 4 = 0 \end{array}\right.$

  在点$(1,1,1)$处的切线和法平面方程。

• 求旋转椭球面$3x^2 + y^2 + z^2 = 16$上点$(-1, -2, 3)$处的切平面与$xOy$面的夹角的余弦。

📌9. 极值与拉格朗日乘数法

无条件极值

对于二元函数$z = f(x,y)$，若存在$P_0(x_0, y_0)$的某个邻域$U(P_0)$，使得$\forall (x, y) \in \mathring{U}(P_0)$，有$f(x, y) < f(x_0, y_0)$($f(x, y)>f(x_0, y_0)$)，则称$P_0(x_0, y_0)$为函数的极大值点(极小值点)，$f(x_0, y_0)$为极大值(极小值)。

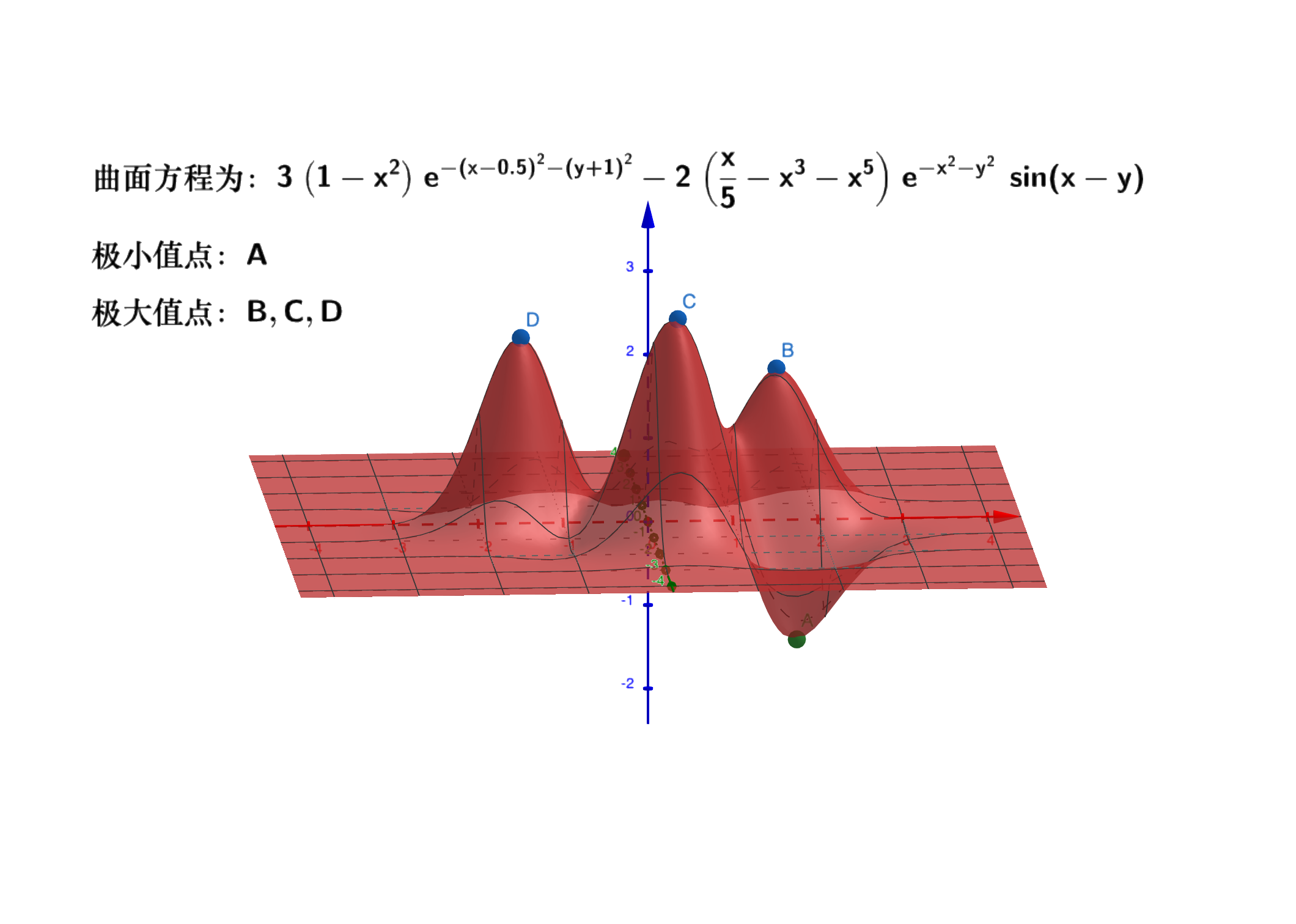
设$z = f(x,y)$在点$P_0(x_0, y_0)$具有偏导数，且在$P_(x_0, y_0)$处有极值，则有：

设$z = f(x,y)$在点$(x_0, y_0)$点的某邻域内连续且具有一阶及二阶连续偏导数，又$f_x(x_0, y_0) = f_y(x_0, y_0) = 0$，令$A = f_{xx}(x_0, y_0), B = f_{xy}(x_0, y_0), C = f_{yy}(x_0, y_0)$，则$f(x,y)$在$(x_0, y_0)$是否取得极值的条件如下：

• $AC - B^2 > 0$时具有极值，且当$A > 0$时为极小值；当$A < 0$时为极大值。

• $AC - B^2 < 0$时没有极值。

• $AC - B^2 = 0$时可能有极值，也可能没有极值。

例子

求函数$f(x,y) = xy(a - x - y)(a \ne 0)$的极值。

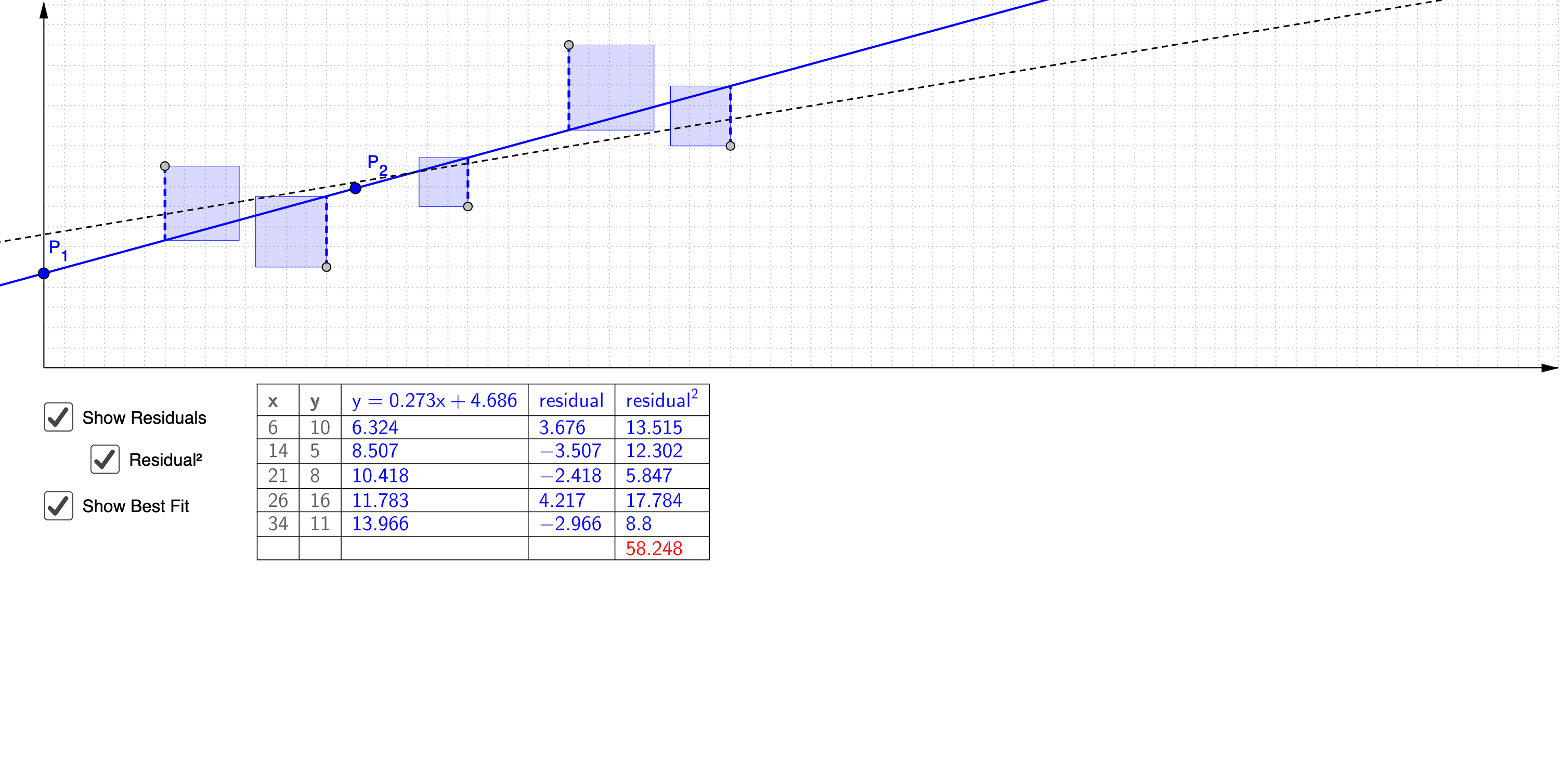
线性最小二乘

设有一组满足线性关系的实验数据：$(x_i, y_i), i = 1,2,\cdots,n$，要确定直线$y=ax + b$使得所有 观测值$y_i$与函数值$ax_i + b$之差的平方和，即：

最小。这种方法称为最小二乘法。

令$\dfrac{\partial E}{\partial a} = 0, \dfrac{\partial E}{\partial b} = 0$，得到：

解这个方程组得到：

线性最小二乘的Python实现

条件极值与拉格朗日乘数法

欲求函数

在约束条件

的极值。

若把条件$\varphi(x,y) = 0$看作$(x,y)$满足的曲线方程，并假设$C$上的点$P_0(x_0, y_0)$为$f$在条件$\varphi(x_0, y_0) = 0$下的极值点，且该条件能够确定一个可微的隐函数$y = g(x)$，则$x_0$必定也是$z = f(x, g(x)) = h(x)$的极值。故由$f$在$P_0$点可微，得到：

而当$\varphi$满足隐函数定理条件时🈶️，

代入得到

上式的几何意义为曲面$z = f(x,y)$的等高线$f(x,y) = f(P_0)$与曲线$C$在$P_0$处具有公共的切线，从而存在某一个常数$\lambda_0$在$P_0$处满足

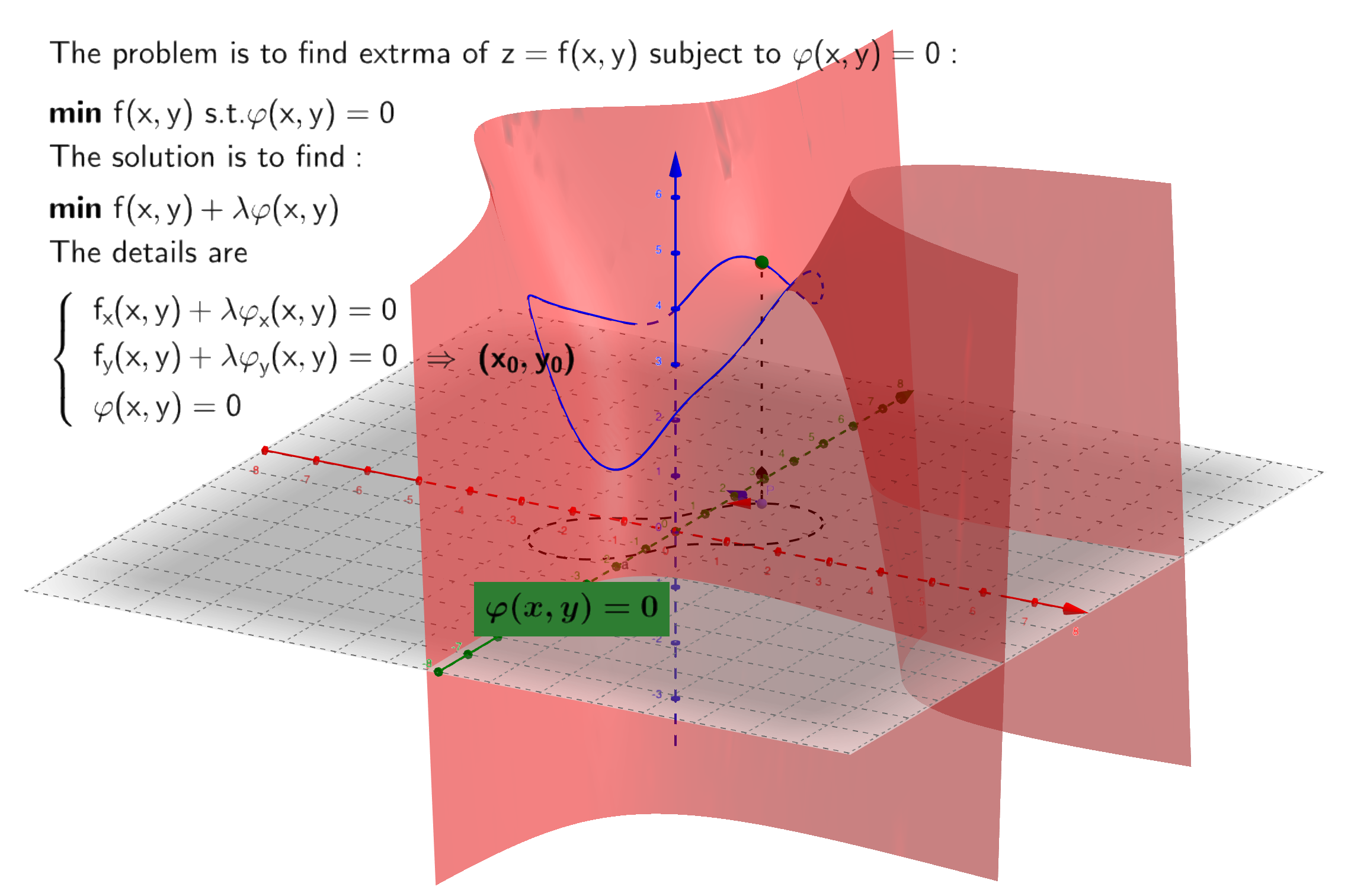
小结

拉格朗日乘数法为，首先由目标函数$f(x,y)$和条件函数$\varphi(x,y) = 0$构造拉格朗日乘数函数：

求解方程组

求得问题的解即可。

例子

求函数

在闭区域

的最大值和最小值。

📚第九次作业:

• 求函数$f(x,y) = 4(x-y) - x^2 - y^2$的极值。

• 抛物面$z = x^2 + y^2$被平面$x + y + z = 1$截成一椭圆，求这椭圆上的点到原点的距离的最大值与最小值。

📚参考书目

📖1. 《高等数学》上下册（第七版），同济大学，高等教育出版社，2014.7.

📖2. 《数学分析》上下册（第二版），陈纪修、於崇华、金路，高等教育出版社，2004.

📖3. 《数学分析》上下册（第二版），华东师范大学数学系，高等教育出版社，2010.

📖4. Mathematical Analysis I,II, 2nd ed. V. A. Zorich, Springer, 2015.

📖5. 数学分析中的典型问题与方法, 裴礼文, 高等教育出版社, 2015.

📖6. Thomas’s Calculus, Weir, Maurice D etc., Addison-Wesley, 2010.

Calculus and its Visualization: an Introduction

👏 THANKS