重积分
Undergraduate course, China University of Petroleum at Beijing, Department of Science, 2020
这部分介绍多元函数重积分及其应用。
目录
📌1. 二重积分的概念与性质
☘︎ 二重积分的概念
考察一个曲顶柱体: 它的底是$xOy$面上的具有零边界的有界区域$D$,顶是非负连续函数$z = f(x,y), (x,y) \in D$所确定的曲面,侧面是以$D$的边界曲线为准线,母线平行于$z$轴的柱面。如下图所示(本图来源于Thomas’ Calculus, 13/e):
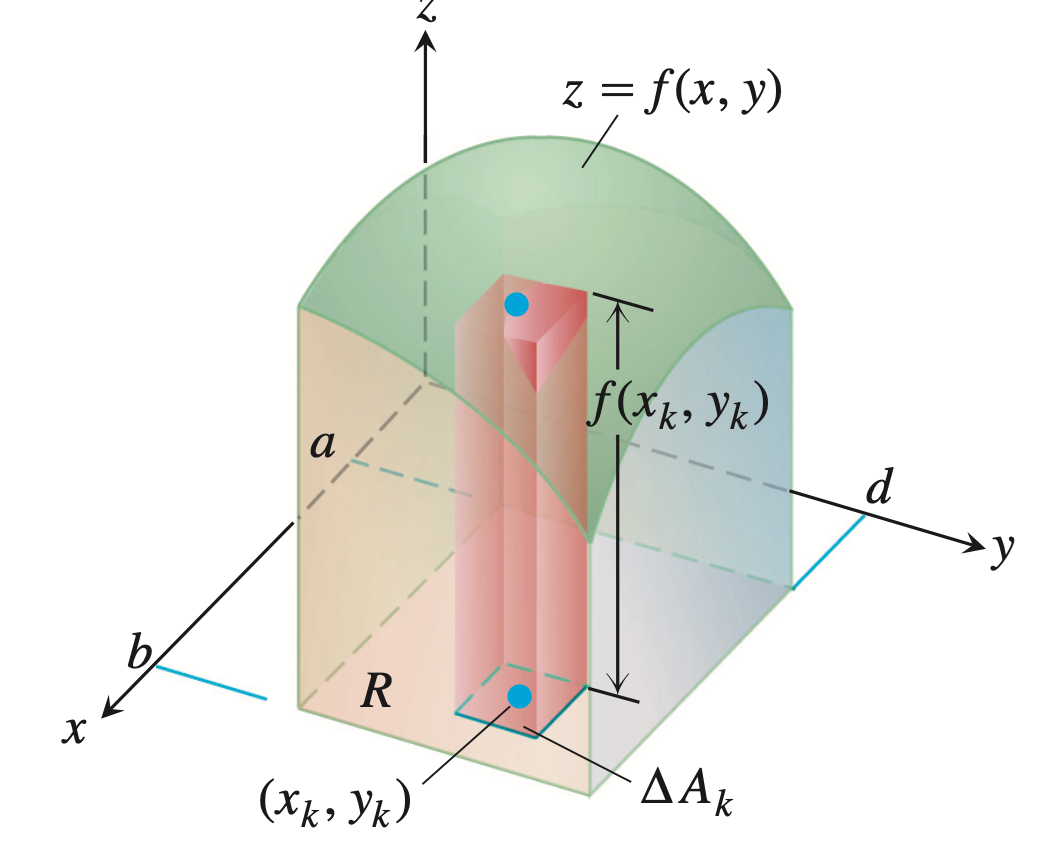
为了得到该曲顶柱体的体积:
- 我们采用一系列平行于坐标轴的直线把区域$D$分割为一系列的小矩形(这个分割记为$P$)。第$k$个小矩形的面积为$\Delta A = \Delta x \Delta y (k=1,2,\cdots,n)$,见下图:
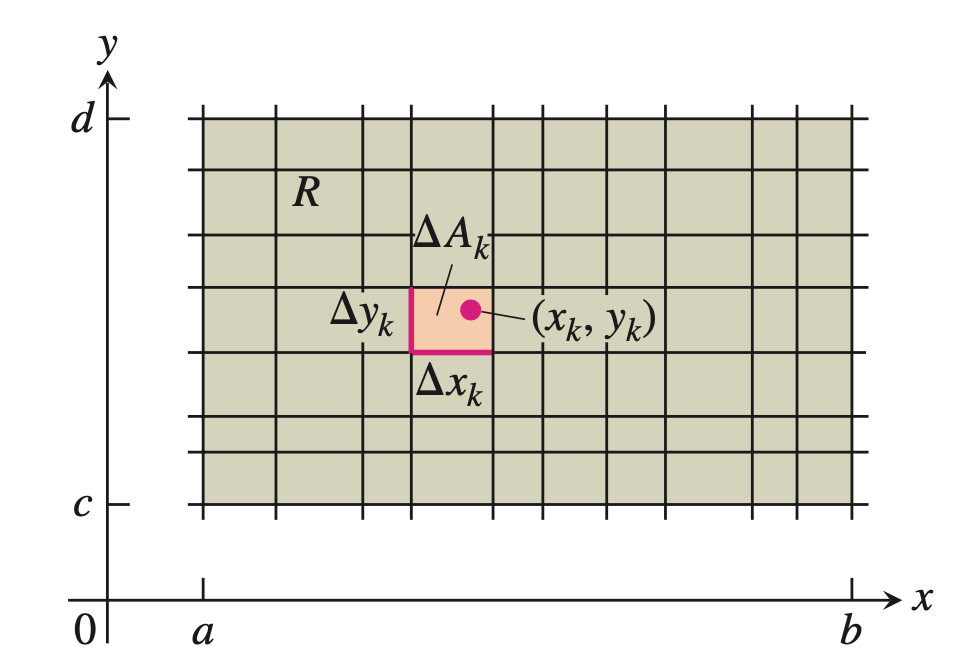
在第$k$个小矩形上任意取一点$(x_k, y_k) \in A_k(k=1,2,\cdots,n)$,然后求和(黎曼和)得到:
$S_n = \sum\limits_{k=1}^n f(x_k, y_k)\Delta A_k$ 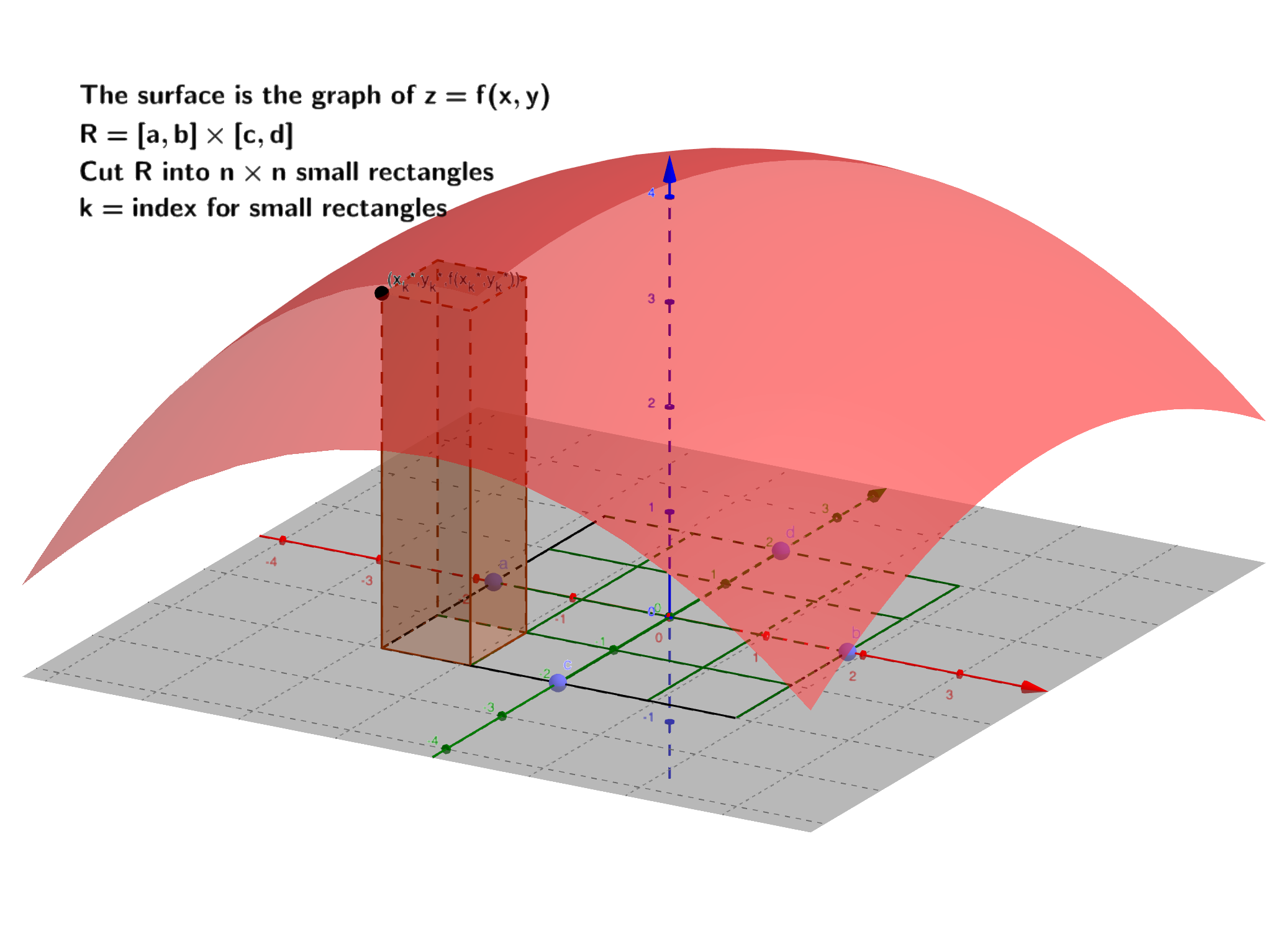
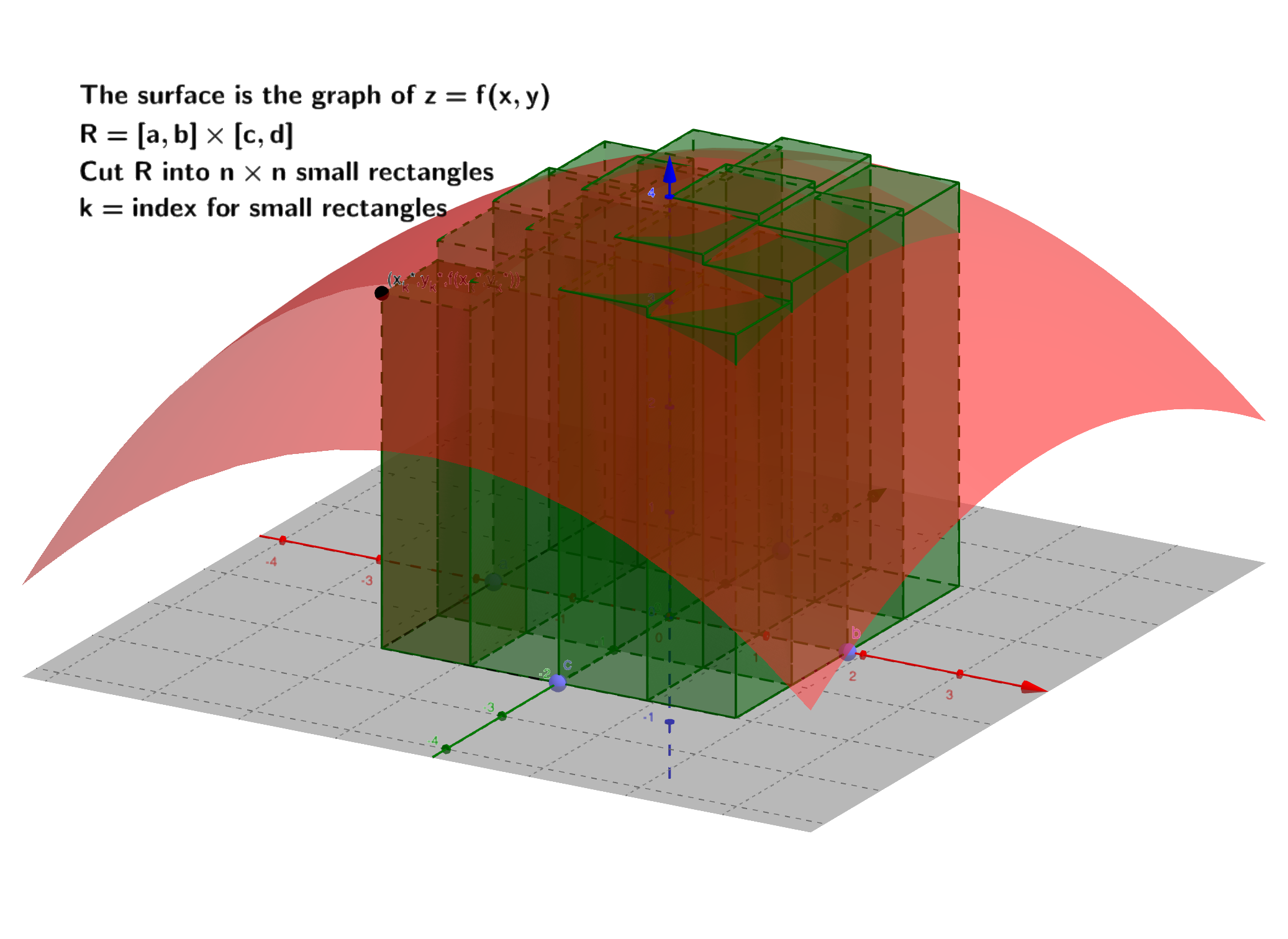
把每个小矩形的直径记为$\lambda_k$,这里直径指的是小矩形中两点连线最长的长度。令
$\Vert P \Vert = \mathbf{max}_{1 \le k \le n}\left\{\lambda_k\right\}$ 称$\Vert P \Vert$为分割细度。黎曼和对分割的细度取极限,讨论极限:
$\lim\limits_{\Vert P \Vert \to 0} \sum\limits_{k=1}^n f(x_k,y_k)\Delta A_k$ 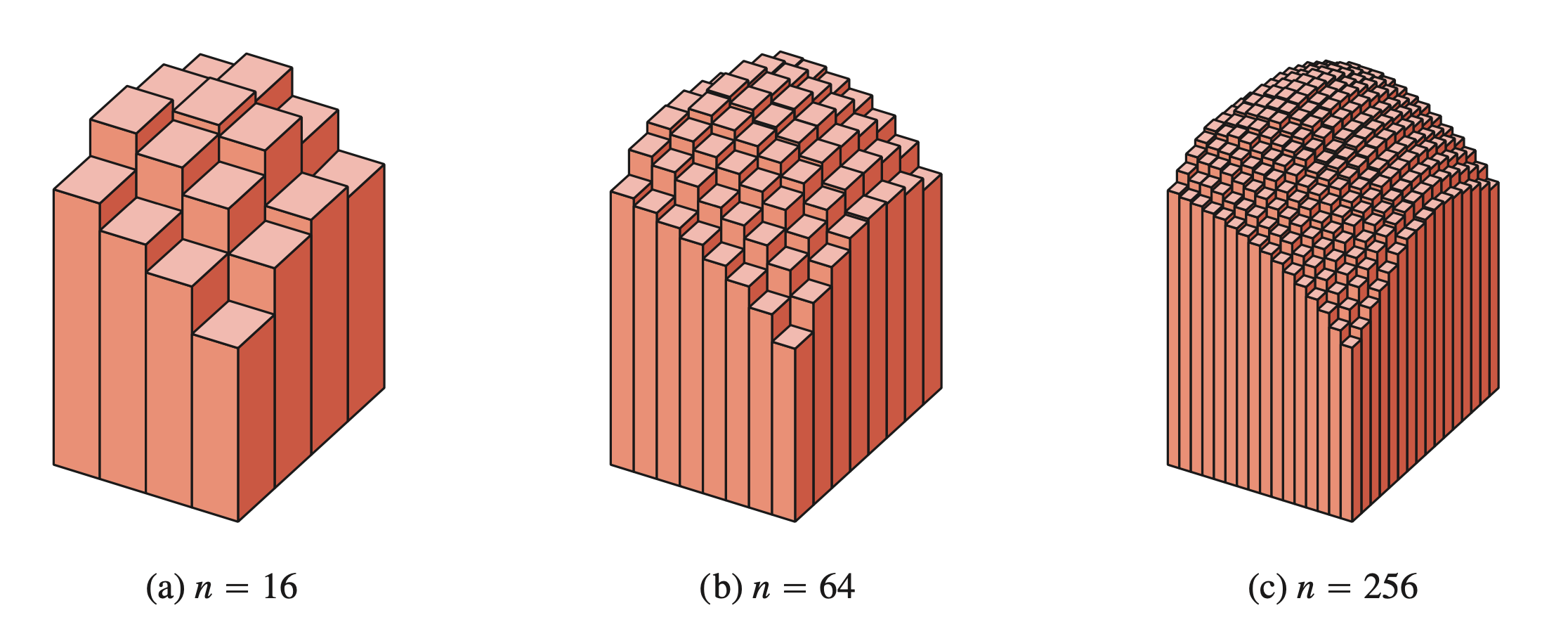
如果随着分割细度趋于零,黎曼和的极限存在,我们称此极限值为$f(x,y)$在$D$上的定积分。记为:
除了采用平行于坐标轴的直线网分割外,也可以采用曲线网分割定义域。不同的分割会得到不同的积分方法。
☘︎二重积分的性质
二重积分$\iint\limits_{D} f(x, y)\mathrm{d}x \mathrm{d}y$具有以下性质:
- 线性:
- 区域可加性:
- 保号性:如果在$D$上,$f(x,y) \le g(x,y)$,那么有:
- 特别的有:
- 设$M \ge f(x,y) \ge m$,则有:
,其中$s(D)$表示区域$D$的面积;
- 中值定理:设函数$f(x,y)$在闭区域$D$上连续,$s(D)$表示区域$D$的面积,则至少存在一点$(\xi, \eta) \in D$满足:
📚第一次作业:
根据二重积分的性质,比较下列积分的大小:
$\iint\limits_{D} (x+y)^2\, \mathrm{d}A$ 与$\iint\limits_{D} (x+y)^3\, \mathrm{d}A$,其中积分区域$D$是由$x$轴,$y$轴与直线$x+y=1$所围成。
$\iint\limits_{D} \ln(x+y)\, \mathrm{d}A$ 与$\iint\limits_{D} \left[\ln(x+y)\right]^2\, \mathrm{d}A$,其中积分区域$D$由$3 \le x \le 5, 0 \le y \le 1$所围成的区域。
根据二重积分的性质,估计下列积分的大小:
$I = \iint\limits_{D} xy(x+y)\, \mathrm{d}\sigma$,其中$D$由$\vert 0 \le x \le 1, 0 \le y \le 1$所围成的区域;
$I = \iint\limits_{D} (x^2 + 4y^2 + 9)\, \mathrm{d}\sigma$,其中$D$由$x^2 + y^2 \le 4$所围成的区域.
📌2. 二重积分的计算方法
下面讨论二重积分$\iint\limits_{D} f(x, y)\mathrm{d}x \mathrm{d}y$的🧮计算问题。
直交坐标下二重积分的计算:Fubini定理
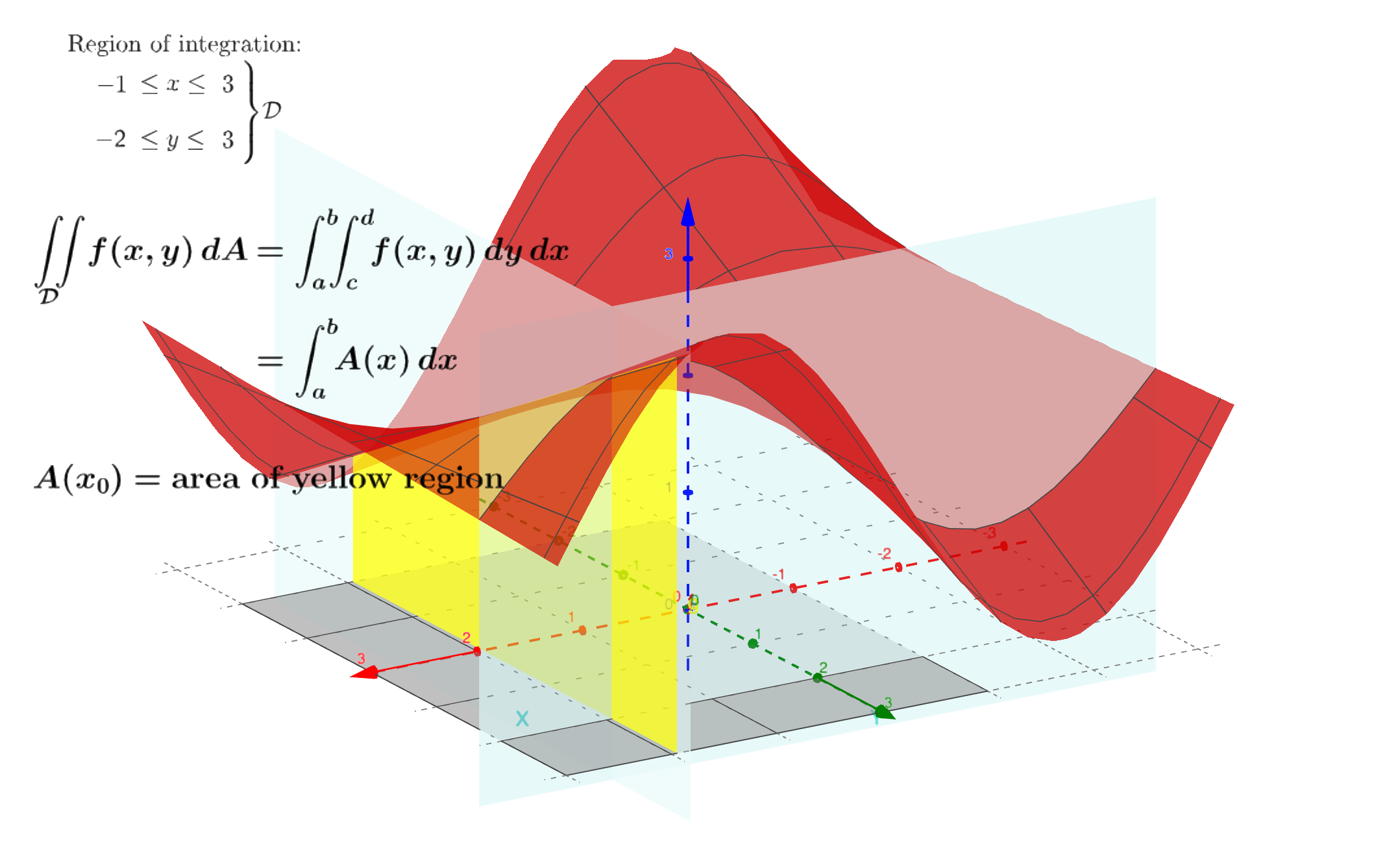
假设我们计算由$z = f(x,y)$在区域$D: -1 \le x \le 3, -2 \le y \le 3$上围成的曲顶柱体的体积。由截面法求体积得到,该曲顶柱体的体积为:
其中$A(x)$为:
将$(2)$式代入$(1)$式得到:
见下图:
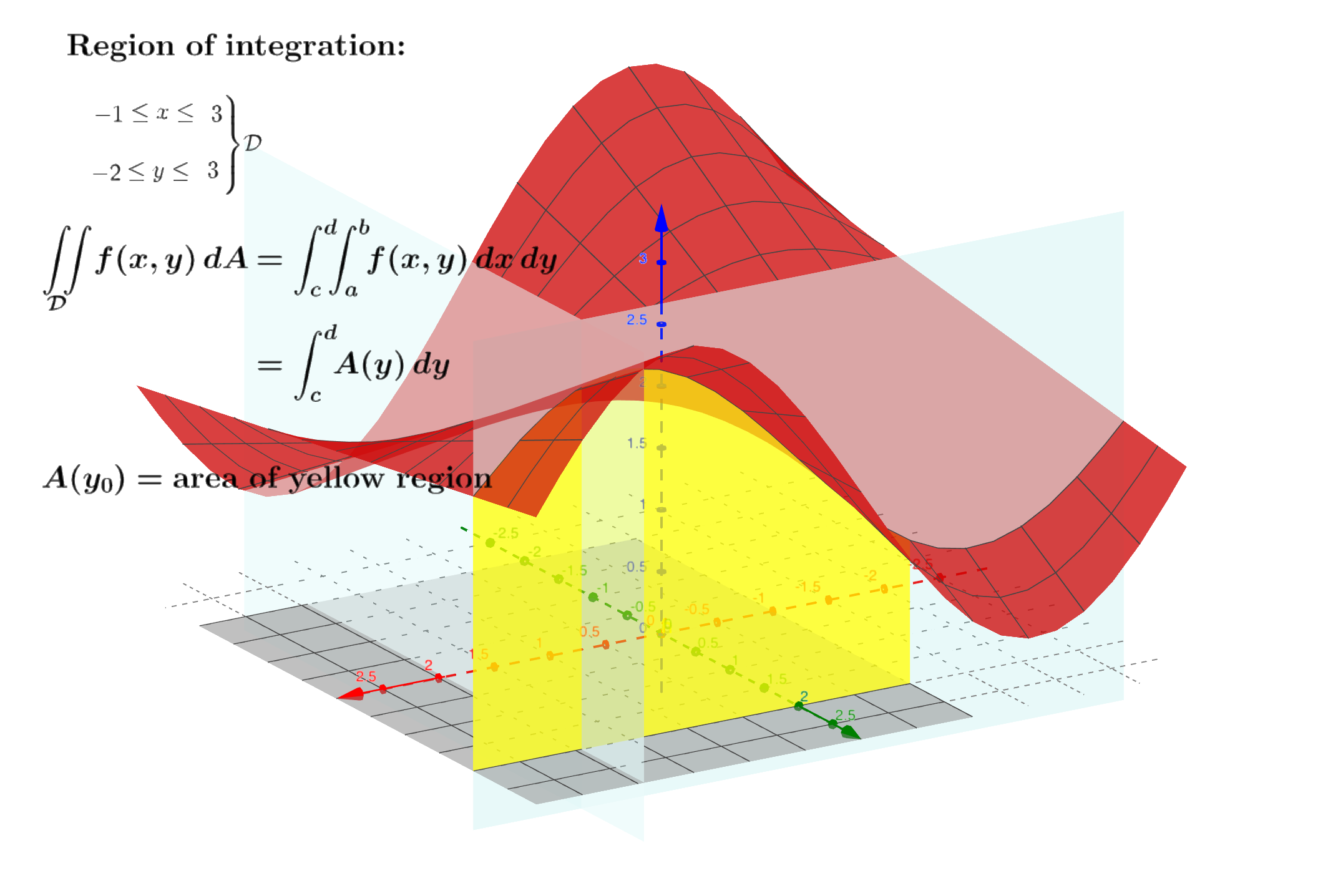
对称地,先对坐标$x$积分,然后对坐标$y$积分,得到:
见下图:
Fubini定理
设$z = f(x,y)$在区域$D: a \le x \le b, c \le y \le d$上连续,则有:
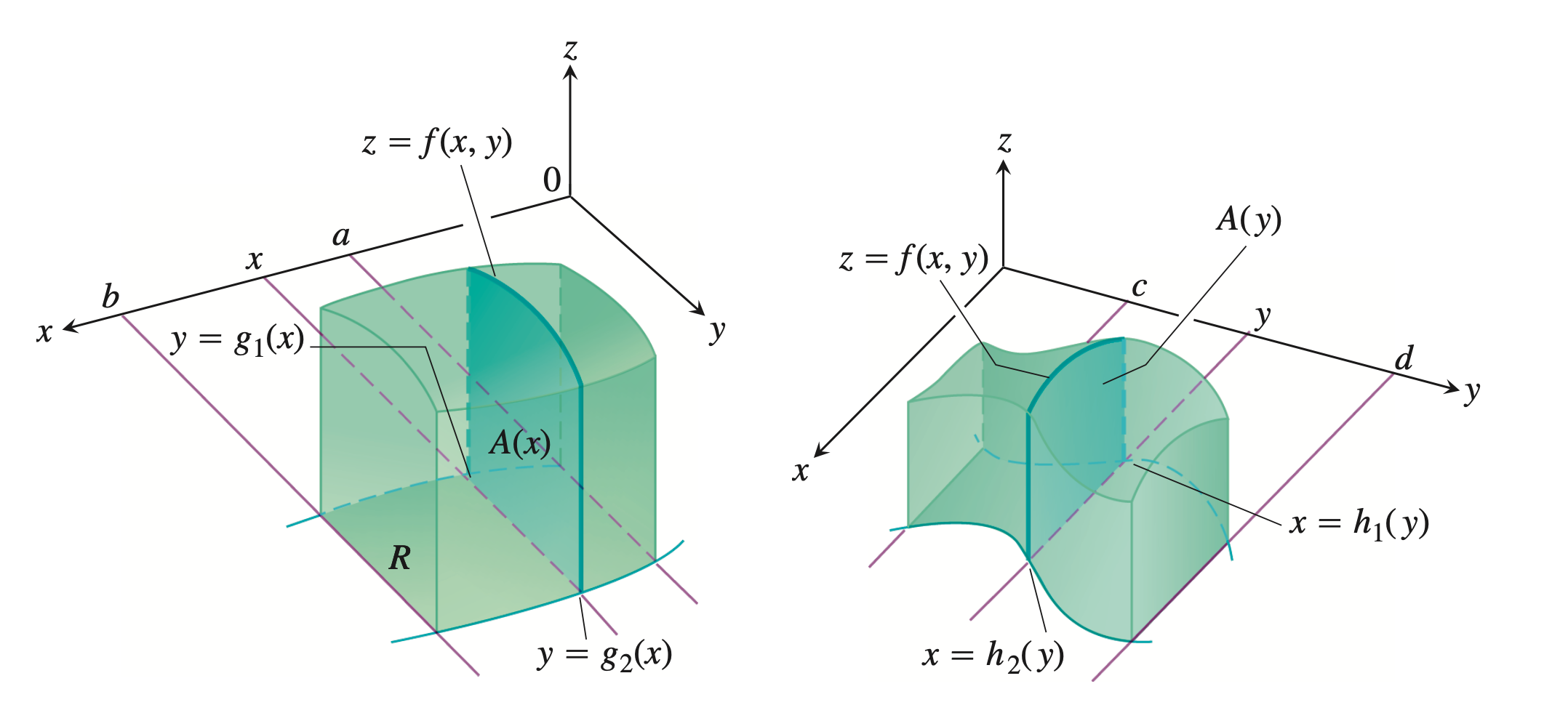
对于一般性区域$D$,分析以下两种情形:
情形一: $D: a \le x \le b, g_1(x) \le y \le g_2(x)$. 对于该类型区域积分可以表示为:
$$\iint\limits_{D}f(x,y)\mathrm{d}x\mathrm{d}y = \int_{a}^b \left(\int_{g_1(x)}^{g_2(x)} f(x,y)\mathrm{d}y\right)\mathrm{d}x \tag {6}$$ 情形二: $D: c \le y \le d, h_1(y) \le x \le h_2(y)$. 对于该类型区域积分可以表示为:
$$\iint\limits_{D}f(x,y)\mathrm{d}x\mathrm{d}y = \int_{c}^d \left(\int_{h_1(y)}^{h_2(y)} f(x,y)\mathrm{d}x\right)\mathrm{d}y \tag {7}$$
见下图(本图来源于Thomas’ Calculus, 13/e):
Fubini定理
设$z = f(x,y)$在区域$D$上连续,如果
$D: a \le x \le b, g_1(x) \le y \le g_2(x)$,这里$g_1(x), g_2(x)$为$[a,b]$上的连续函数, 则有:
$\iint\limits_{D}f(x,y)\mathrm{d}x\mathrm{d}y = \int_{a}^b \left(\int_{g_1(x)}^{g_2(x)} f(x,y)\mathrm{d}y\right)\mathrm{d}x$ $D: c \le y \le d, h_1(y) \le x \le h_2(y)$,这里$h_1(x), h_2(x)$为$[c,d]$上的连续函数,则有:
$\iint\limits_{D}f(x,y)\mathrm{d}x\mathrm{d}y = \int_{c}^d \left(\int_{h_1(y)}^{h_2(y)} f(x,y)\mathrm{d}x\right)\mathrm{d}y$
✏️例子
计算$\iint\limits_{D}xy\mathrm{d}x\mathrm{d}y$,其中$D$是由直线$y = 1, x = 2, y = x$所围成的闭区域。
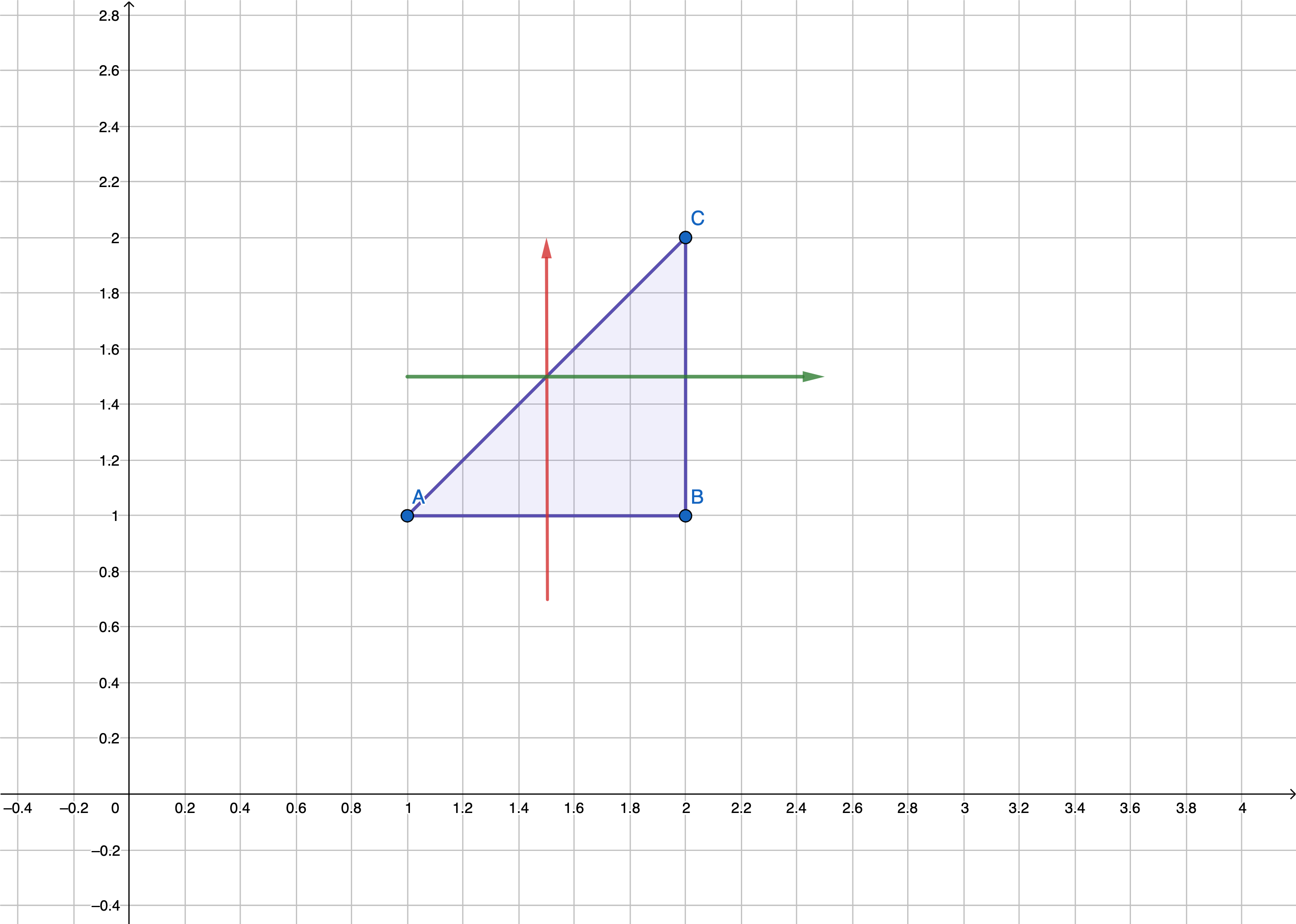
✏️例子
计算积分$\iint\limits_{R} \dfrac{\sin x}{x}\mathrm{d}x\mathrm{d}y$,其中$R$由$x$轴$y=x$及$x=1$围成的闭区域。
✏️例子
求两个圆柱面$x^2 + y^2 = R^2, x^2 + z^2 = R^2$所围成立体的体积。

✏️例子
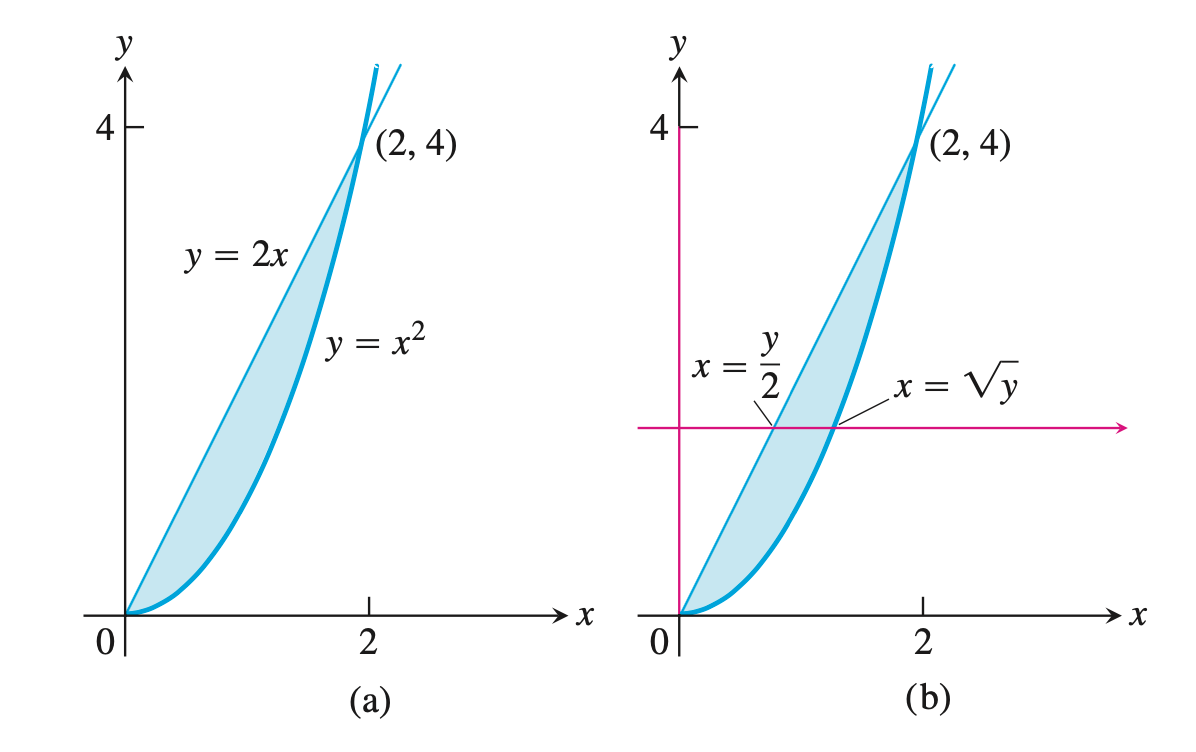
交换积分的顺序$\int_0^2 \int_{x^2}^{2x}(4x + 2)\mathrm{d}y \mathrm{d}x$
极坐标下二重积分的计算
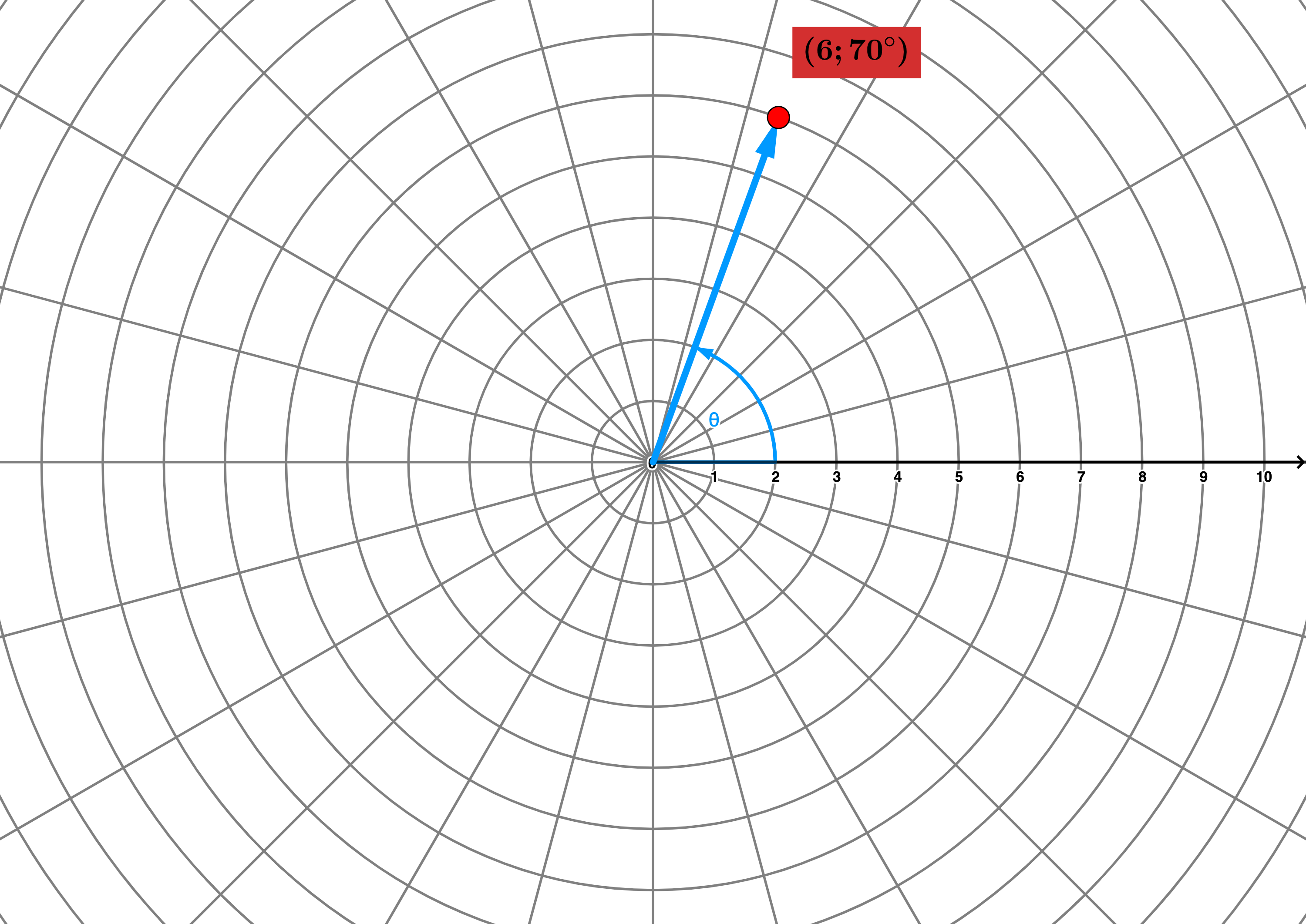
极坐标
平面上的点可以用直角坐标$(x,y)$表示,也可以用极坐标$(r, \theta)$表示,见下图:
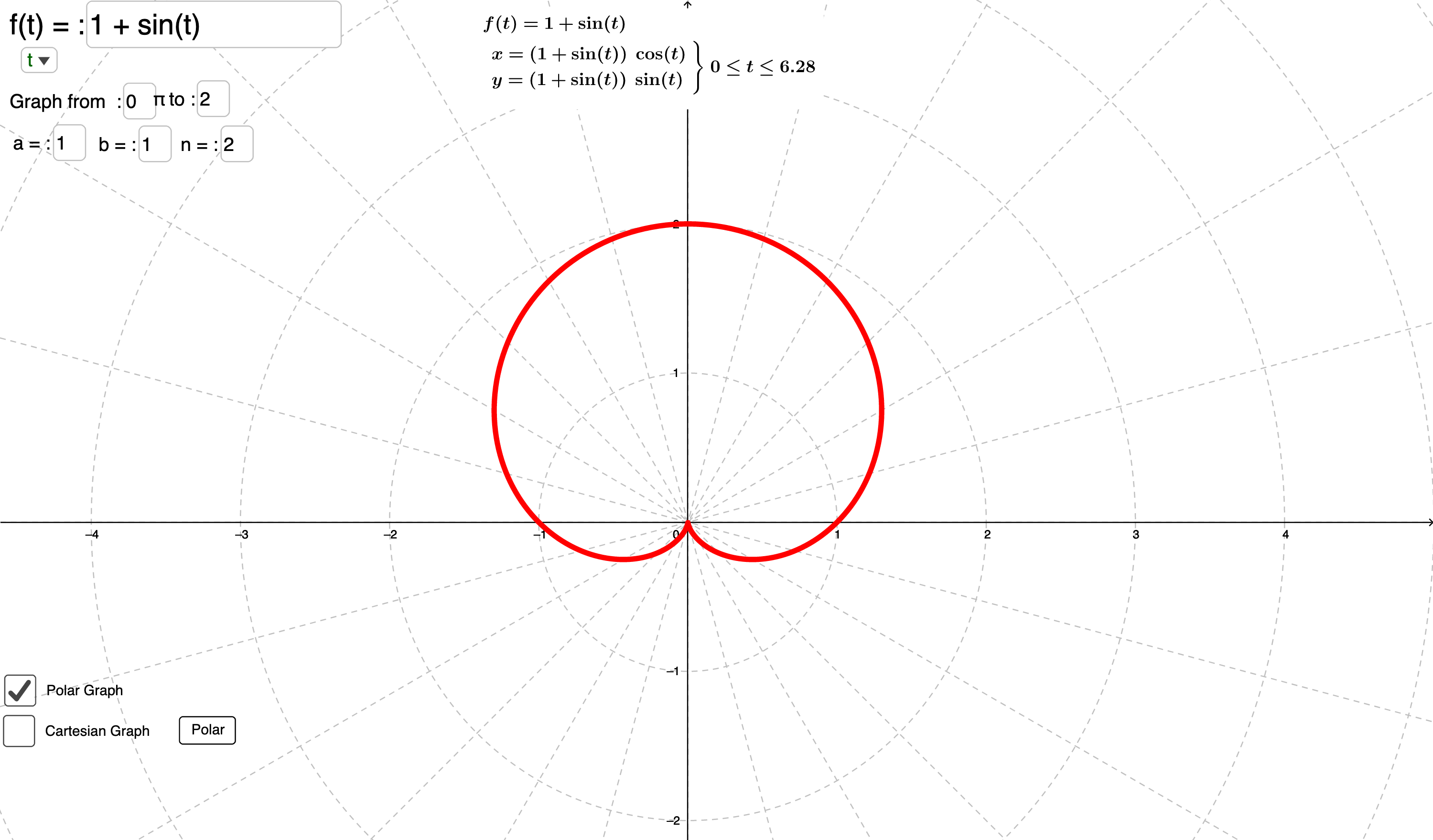
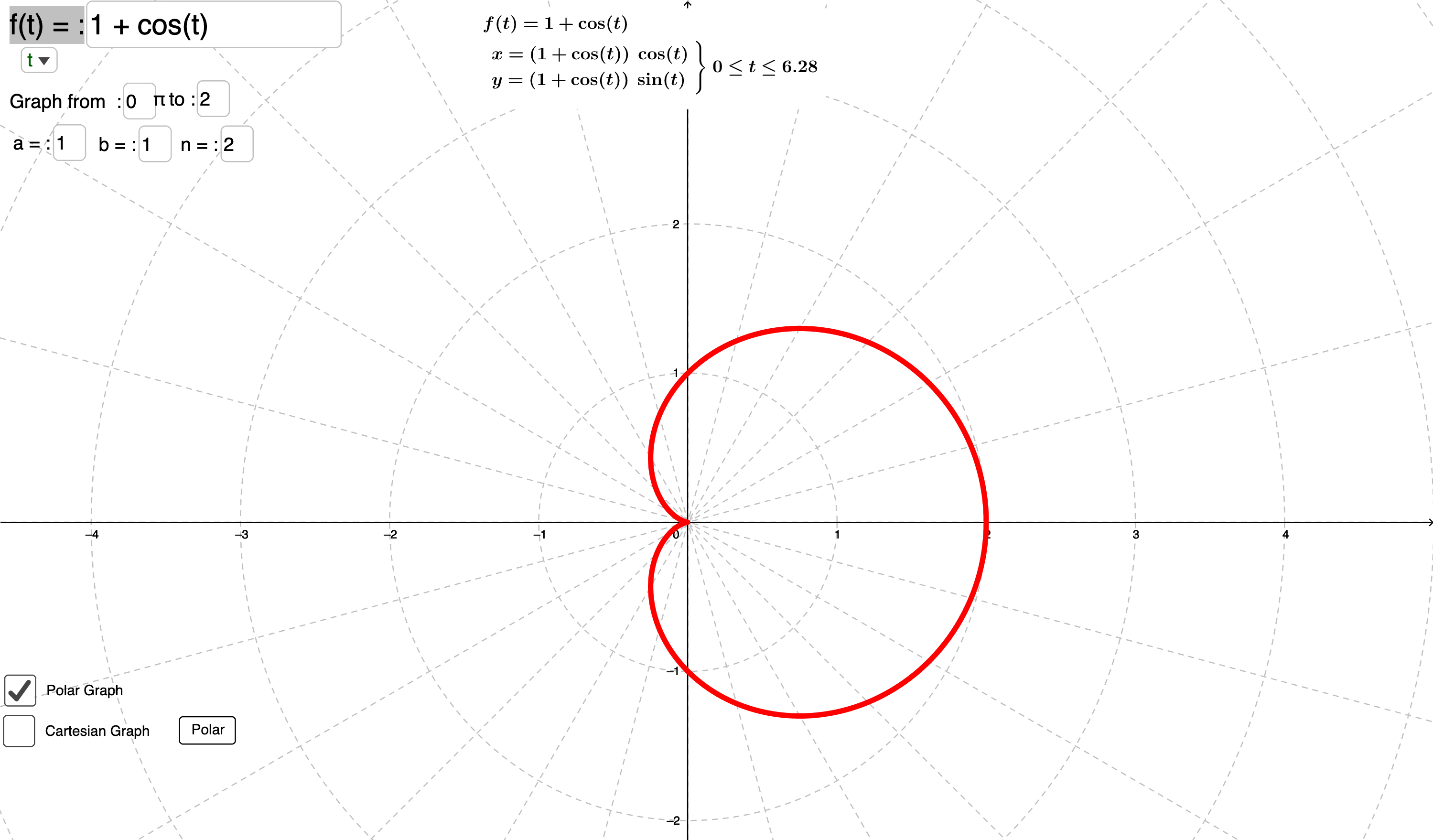
极坐标系下求区域的面积
定积分为求解不规则问题的一种方法,该方法简而言之可概括为“分割,取近似(微分或者线性化),求和,取极限。”
求曲边梯形的面积:$\int_a^b f(x)\mathrm{d}x = \int_a^b \mathrm{d}F(x)$,积分为微分的累加,而微分为所求问题增量的线性近似。
下面探讨极坐标下图形的面积:
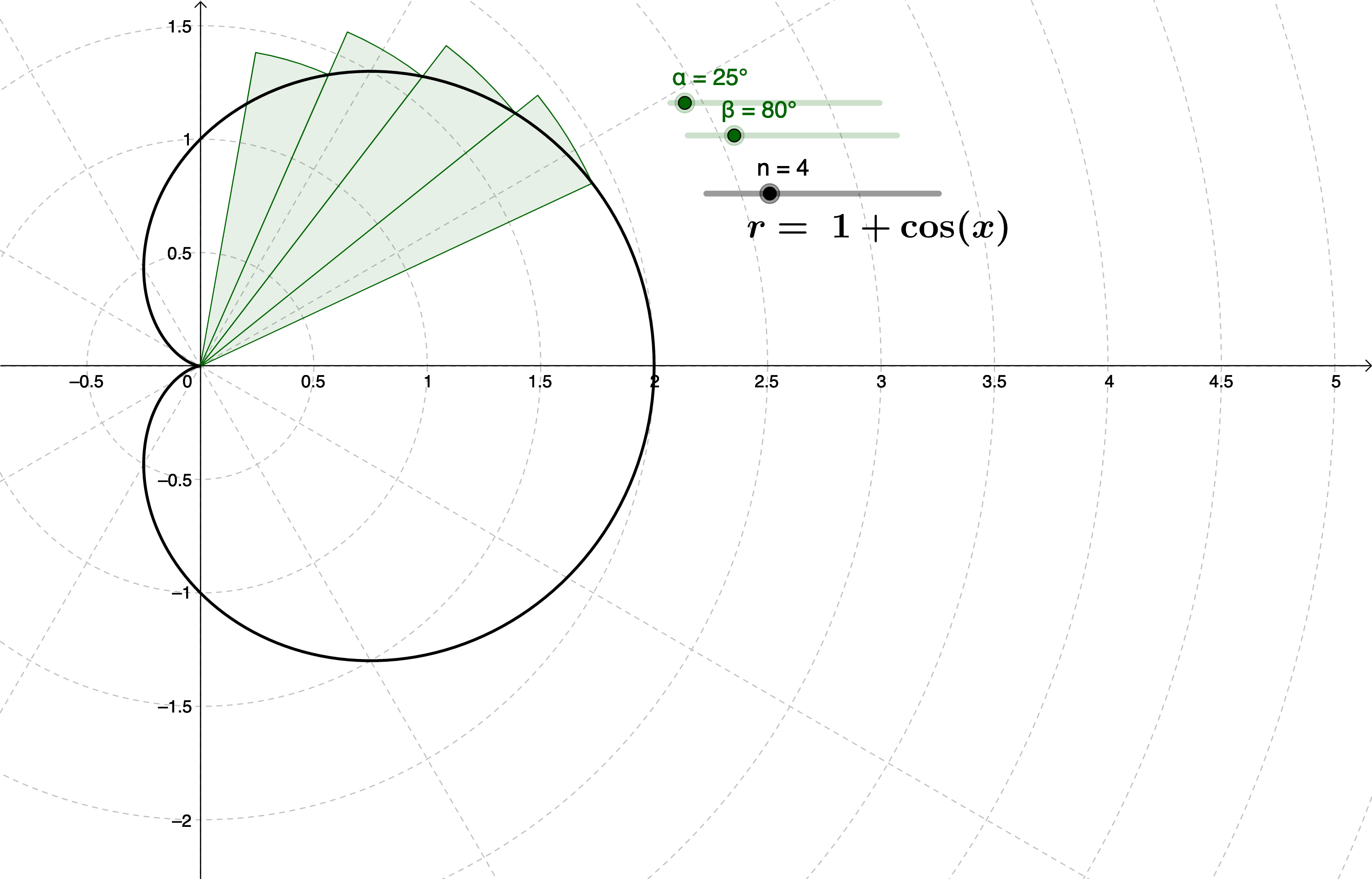
$S = \int_{\alpha}^{\beta}\dfrac{1}{2}r^2(\theta)\mathrm{d}\theta$
极坐标下求二重积
首先推导一下极坐标下求二重积分。设区域$R: \alpha \le \theta \le \beta, g_1(\theta) \le r \le g_2(\theta)$。采用
分割该区域,则定义在区域$R$上的二重积分可以近似的表示为:
这里$\Delta A_k$表示第$k$块小区域的面积,$r_k, \theta_k$为在地$k$块区域上的取值。见下图:
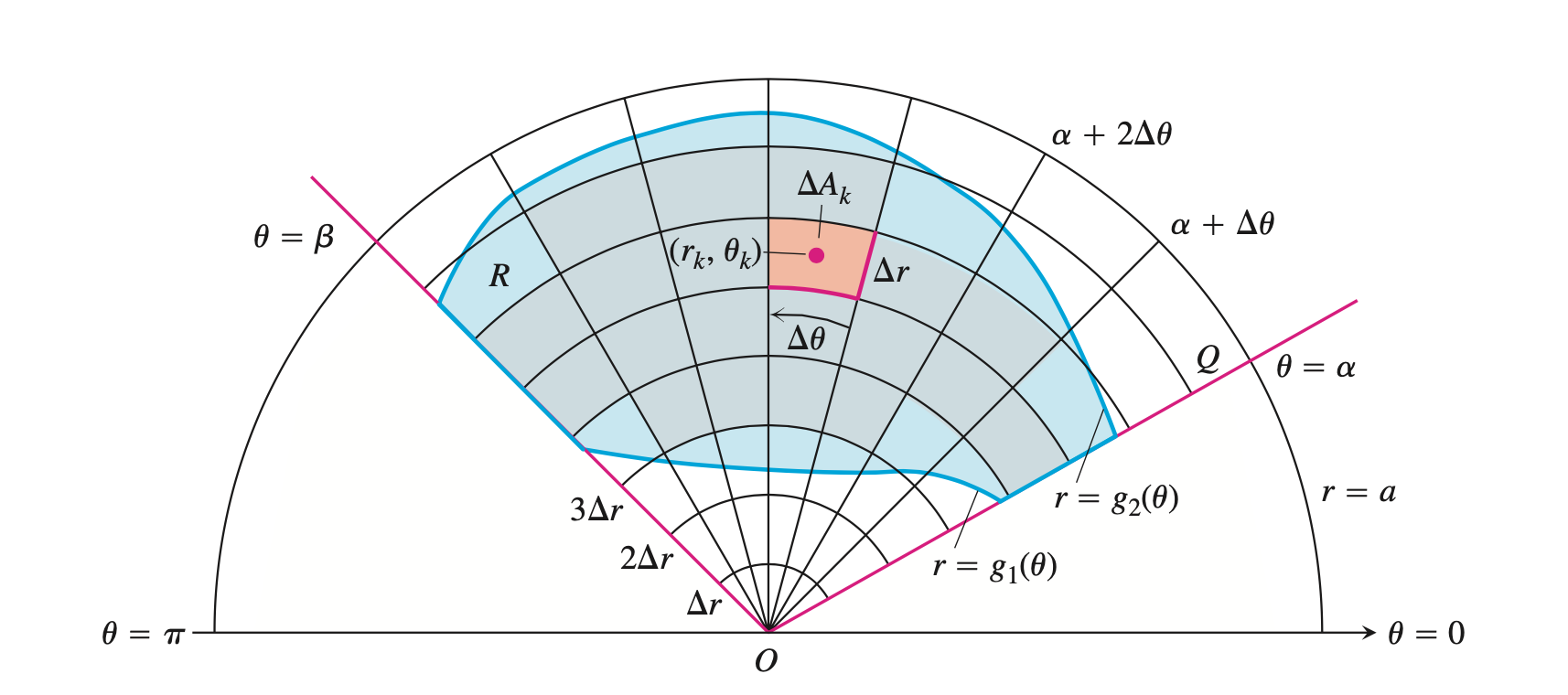
二重积分可表示为:
接下来我们来分析$(8)$式中$\mathrm{d}A$的表示。
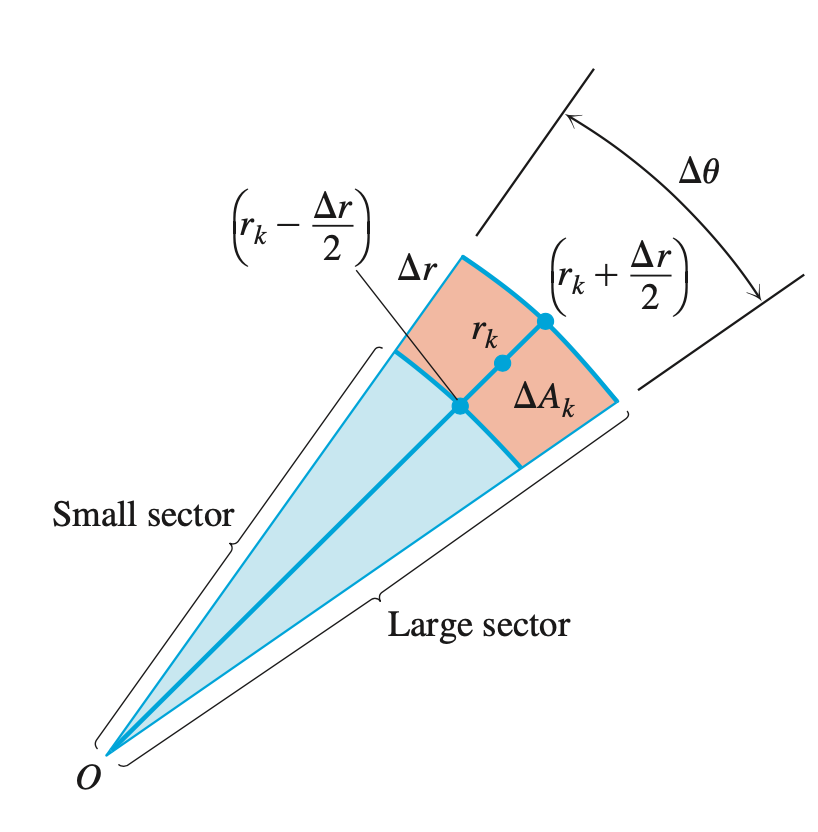
所以有:
故
确定积分范围的步骤
画出图形,写出边界曲线方程和交点的坐标;
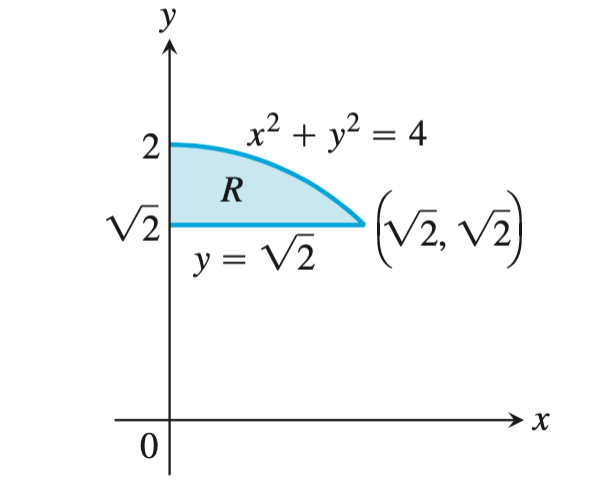
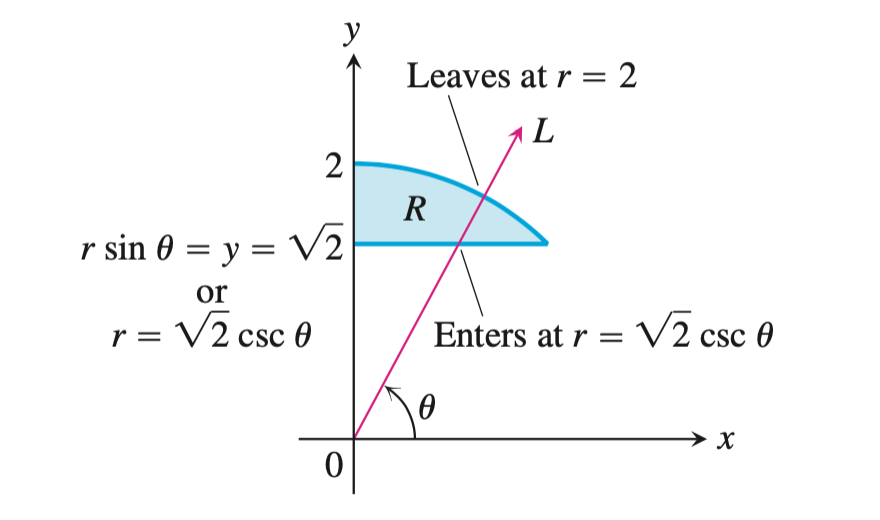
找到极坐标中$r$的上下限,通俗的讲,找到极径的起始穿入边界和终止穿出边界。
找到极坐标中$\theta$的上下限,找到$\theta$的最小、最大值使积分区域落入该区域中。
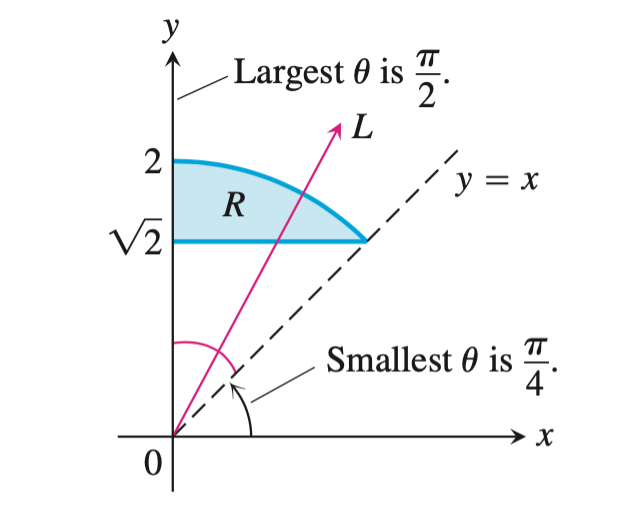
写出积分表达式:
$\iint\limits_{R} f(x,y)\mathrm{d}A = \int_{\dfrac{\pi}{4}}^{\dfrac{\pi}{2}} f(r, \theta) r \mathrm{d}r\mathrm{d}\theta$ ✏️例子
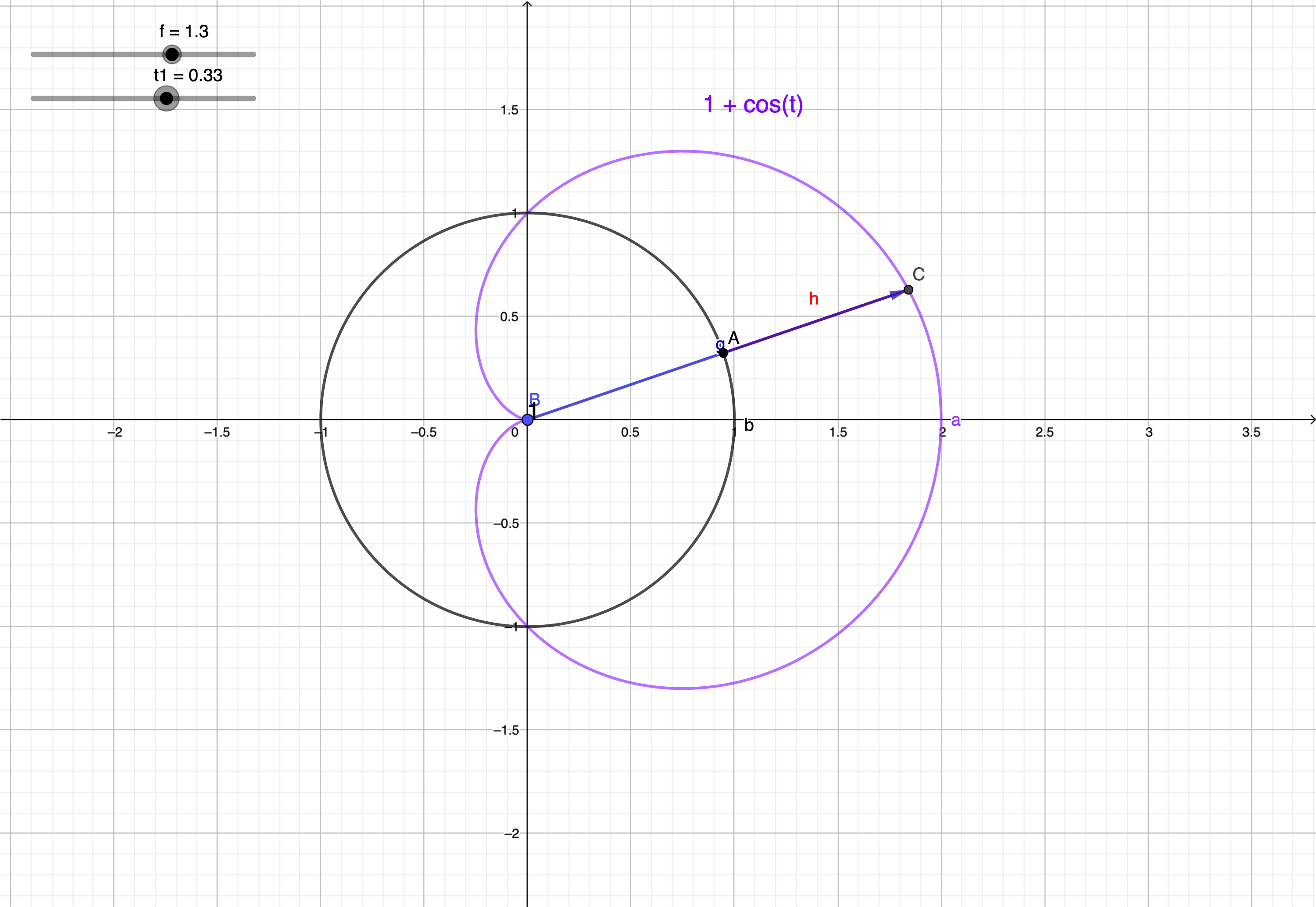
求位于曲线$r = 1$的外面,$r = 1 + \cos \theta$内部区域的面积。
✏️例子
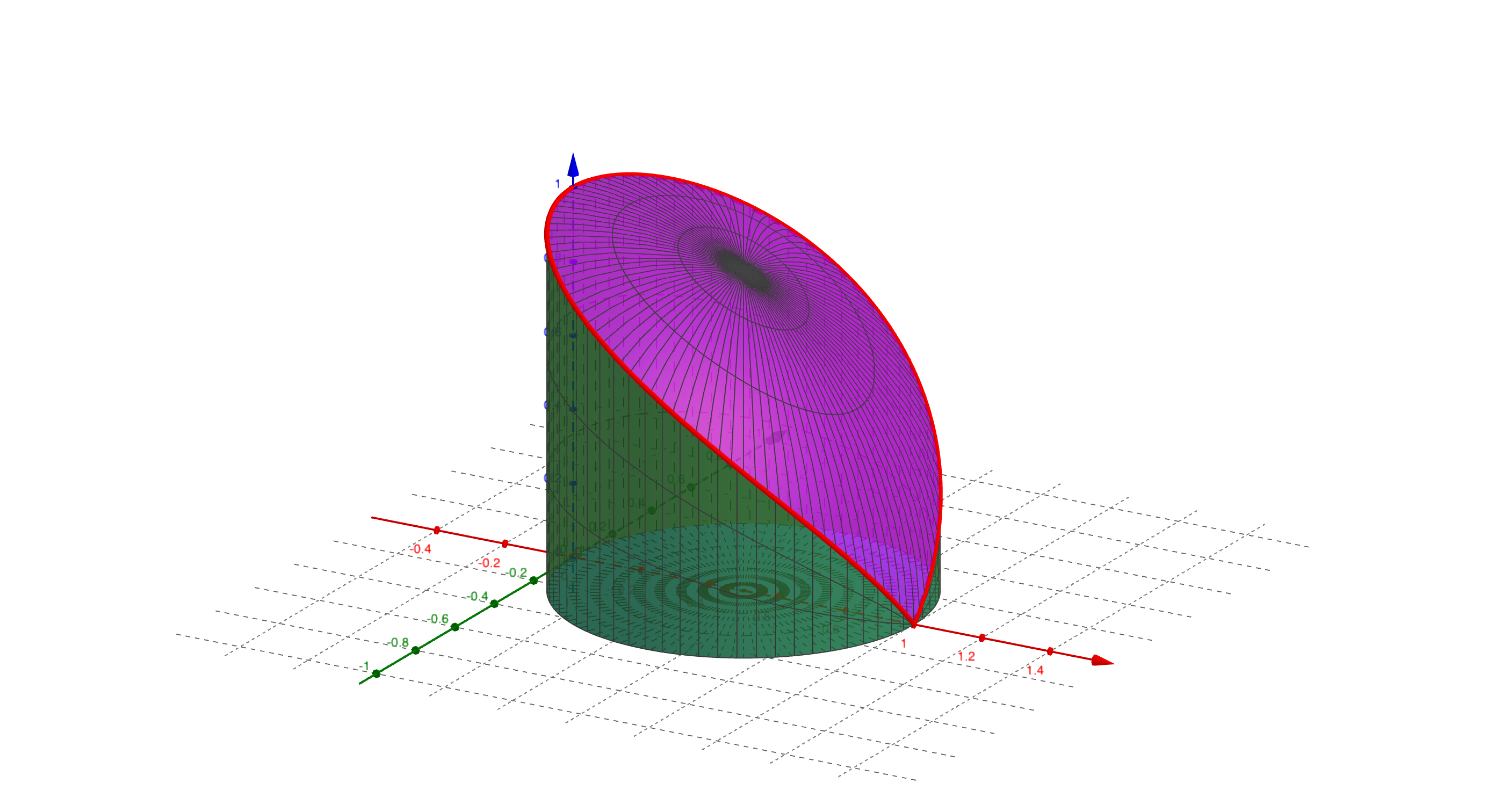
求球体$x^2 + y^2 + z^2 \le 4R^2$被圆柱面$x^2 + y^2=2Rx(R>0)$所截所得的(含在圆柱面内的部分)立体的体积。见下图:
✏️例子
转换直角坐标为极坐标积分$\int_0^{+\infty}\int_0^{+\infty} e^{-x^2 - y^2}\,\mathrm{d}x\,\mathrm{d}y$,并计算泊松积分$\int_0^{+\infty} e^{-x^2}\, \mathrm{d}x$
📚第二次作业:
设$f(x,y)$在区域$D$上连续,试将二重积分$\iint\limits_{D}f(x,y)\,\mathrm{d}A$化为不同顺序的累次积分:
$D$由不等式$0 \le x \le 2, x \le y \le 2x$所围成的区域;
$D$由不等式$y \le x, y \ge 0, x^2 + y^2 \le 1$所围成的区域;
$D$由不等式$x^2 + y^2 \le 1, x+y \ge 1$所围成的区域;
$D$由不等式$\vert x \vert + \vert y \vert \le 1$所围成的区域.
改变下列累次积分的顺序:
$\int_{-1}^{1}\, \mathrm{d}x \int_{-\sqrt{1-x^2}}^{1-x^2}f(x,y)\,\mathrm{d}y$;
$\int_{0}^{2a}\, \mathrm{d}x \int_{\sqrt{2ax-x^2}}^{\sqrt{2ax}}f(x,y)\,\mathrm{d}y$;
$\int_{0}^{1}\, \mathrm{d}x \int_{0}^{x^2}f(x,y)\,\mathrm{d}y + \int_{1}^{3}\,\mathrm{d}x\int_0^{\dfrac{1}{2}(3-x)} f(x,y)\,\mathrm{d}y$.
计算下列二重积分
$\iint\limits_{D}x\sqrt{y}\, \mathrm{d}A$,其中$D$由抛物线$y = \sqrt{x},y = x^2$所围成的区域;
$\iint\limits_{D}xy^2\, \mathrm{d}A$,其中$D$由圆周$x^2 + y^2 = 4$及$y$轴所围成的圆周的右半部分;
$\iint\limits_{D}e^{x+y}\, \mathrm{d}A$,其中$D$由圆周$\vert x \vert + \vert y \vert \le 1$所围成的区域;
化下列二次积分为极坐标的累次积分:
$\int_0^1\,\mathrm{d}x\int_0^1f(x,y)\,\mathrm{d}y$;
$\int_0^2\,\mathrm{d}x\int_x^{\sqrt{3x}}f(\sqrt{x^2+y^2})\,\mathrm{d}y$;
$\int_0^1\,\mathrm{d}x\int_{1-x}^{\sqrt{1-x^2}}f(x,y)\,\mathrm{d}y$;
$\int_0^1\,\mathrm{d}x\int_0^{x^2}f(x,y)\,\mathrm{d}y$;
计算下列二重积分(极坐标系):
$\int_0^{2a}\,\mathrm{d}x\int_0^{\sqrt{2ax-x^2}}x^2 + y^2\,\mathrm{d}y$;
$\int_0^{a}\,\mathrm{d}x\int_0^x \sqrt{x^2 + y^2}\,\mathrm{d}y$;
$\iint\limits_{D} e^{x^2 + y^2}\,\mathrm{d}A$,其中$D$由圆周$x^2 + y^2 \le 4$所围成的区域.
📌3. 三重积分
假设$F(x,y,z)$为定义在空间区域$D$上的一个连续函数(比如说是密度函数),采用平行于坐标平面的平面网分割区域$D$。在第$k$个小长方体任意取一点$(x_k, y_k, z_k) \in \Delta V_k$,该长方体的边长分别为$\Delta x, \Delta y, \Delta z$。作和式:
如果当分割的细度趋于零时,上式的极限存在,即
存在,我们称$F(x, y, z)$在$D$上可积,记为:
直角坐标下计算三重积分
计算步骤如下:
画出积分区域,并画出在坐标平面上的投影区域。
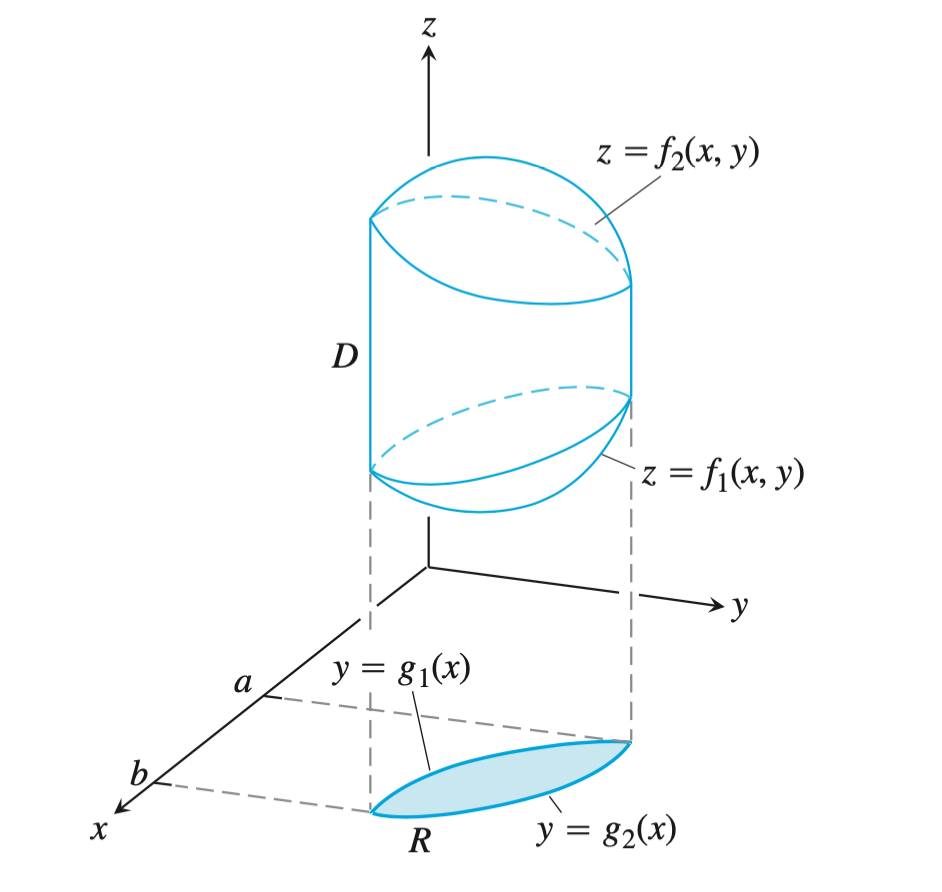
在投影区域上选取一点$(x,y)$,平行于$z$轴作射线,找到区域$D$的穿入曲面(积分的下限)和穿出曲面(积分的上限)。
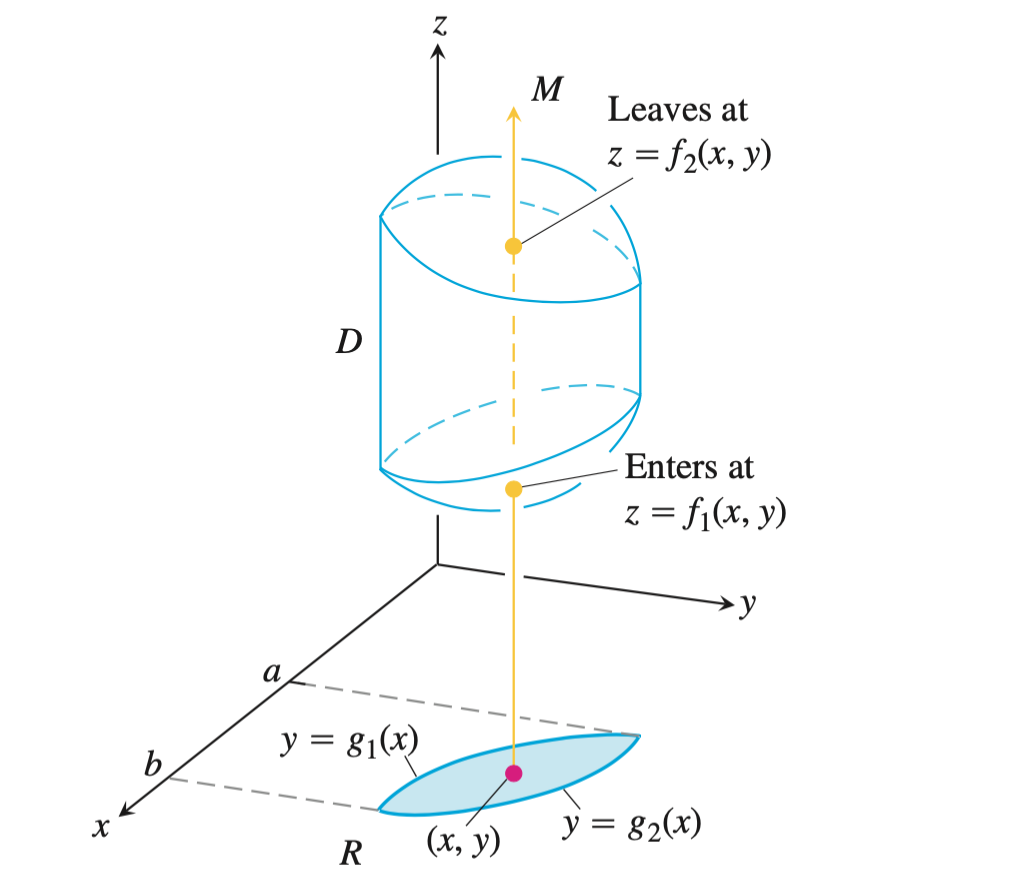
在投影区域上$R$作射线,找到$y$的穿入边界和穿出边界。下图:射线的穿入边界为$g_1(x)$,穿出边界为$g_2(x)$。这些是$y$的积分上下限。
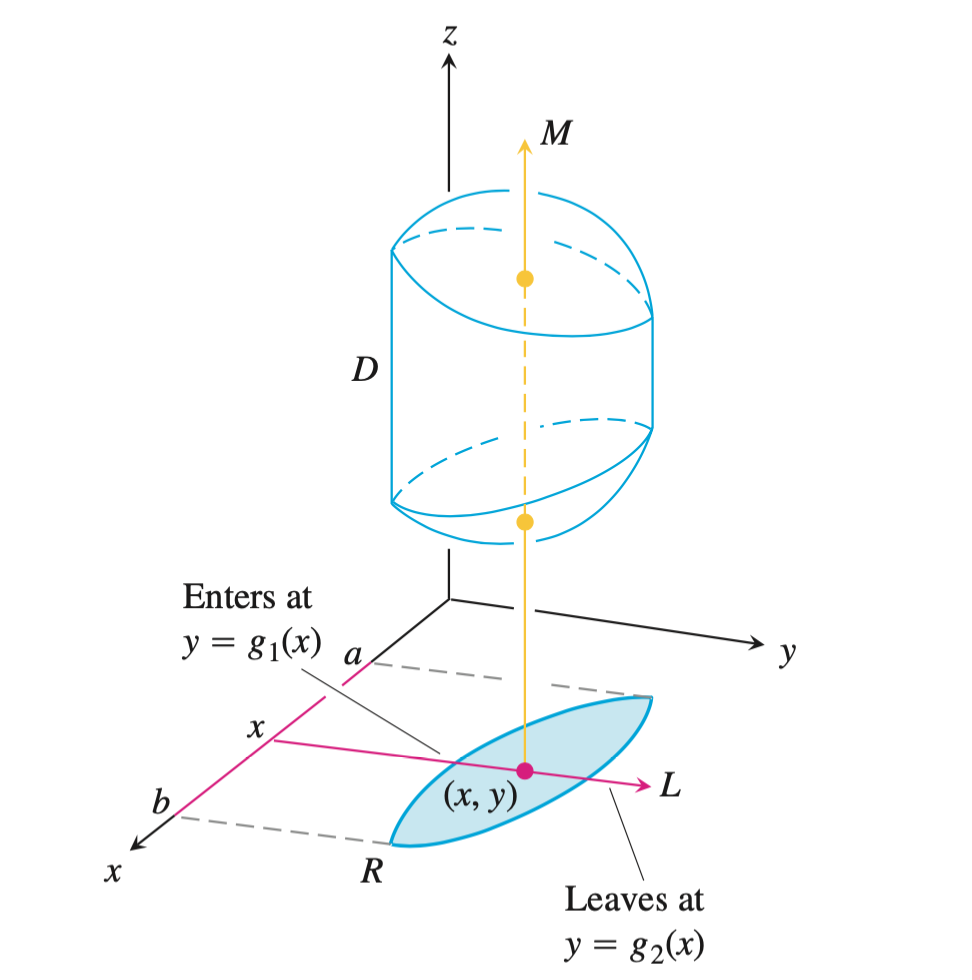
找到$x$的变换范围,最后将重积分转化为累次积分:
$\iiint\limits_{D}F(x,y,z)\,\mathrm{d}V = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{f_1(x,y)}^{f_2(x,y)} F(x,y,z)\,\mathrm{d}z\,\mathrm{d}y\,\mathrm{d}x$
✏️例子
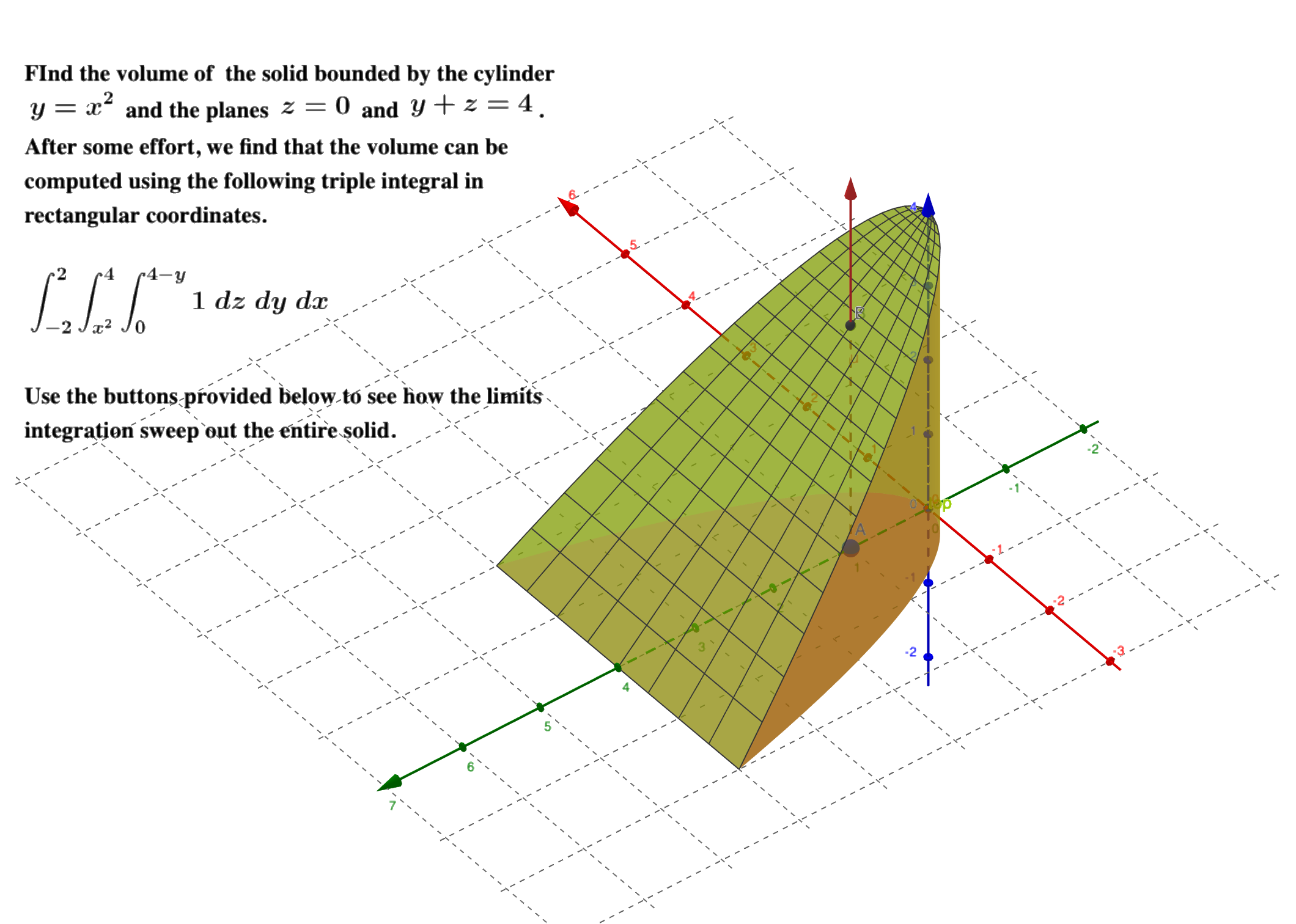
✏️例子
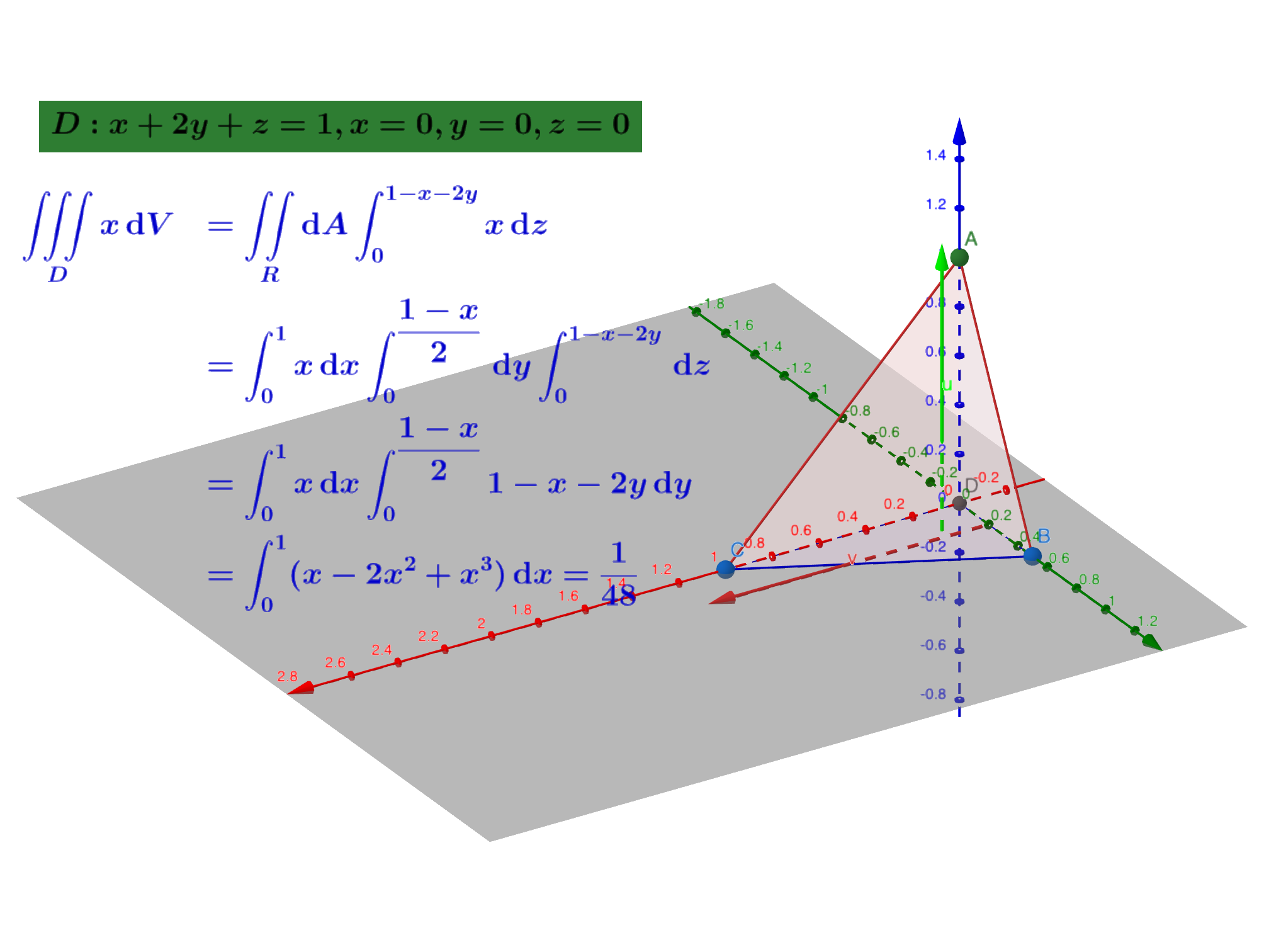
✏️例子
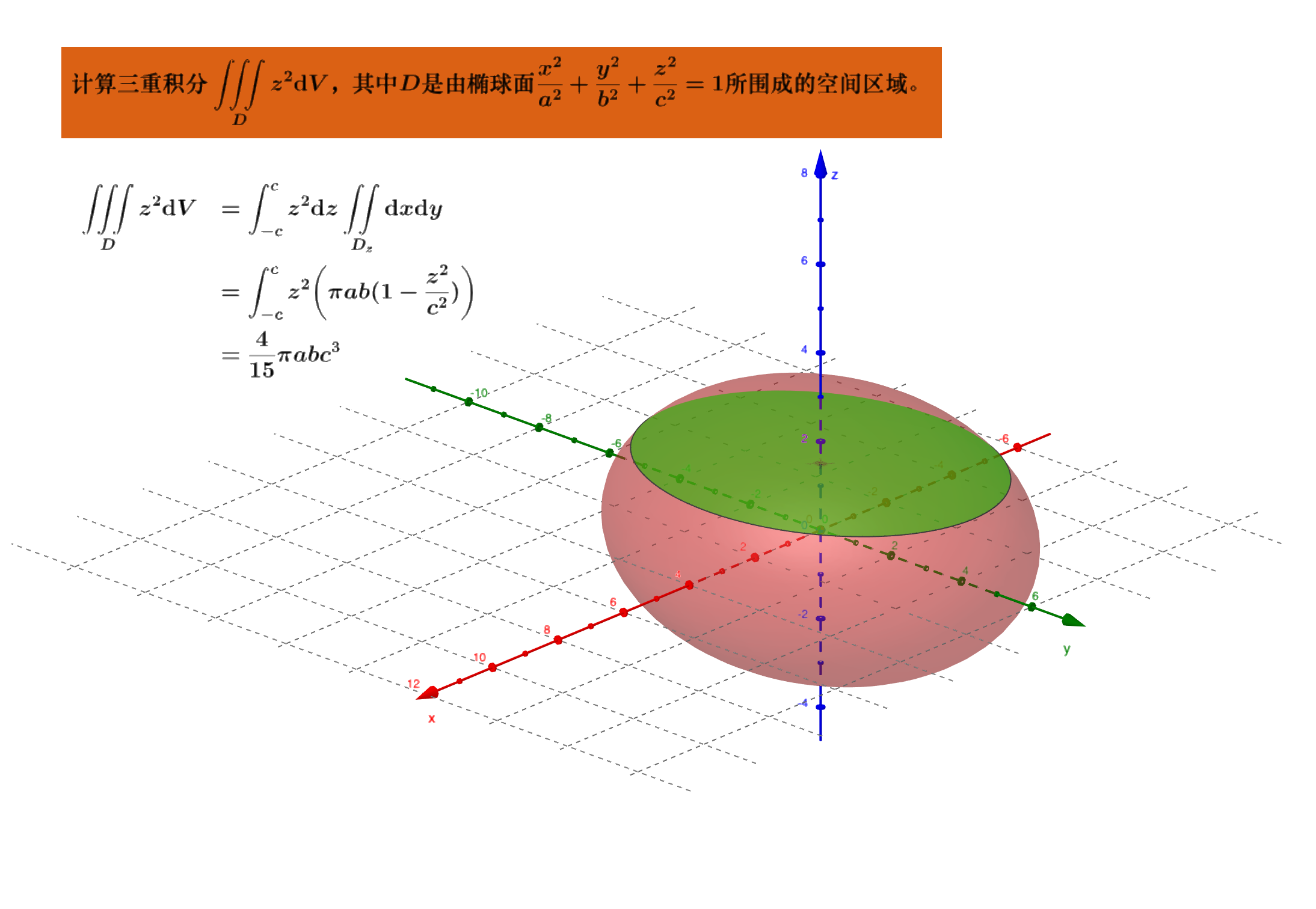
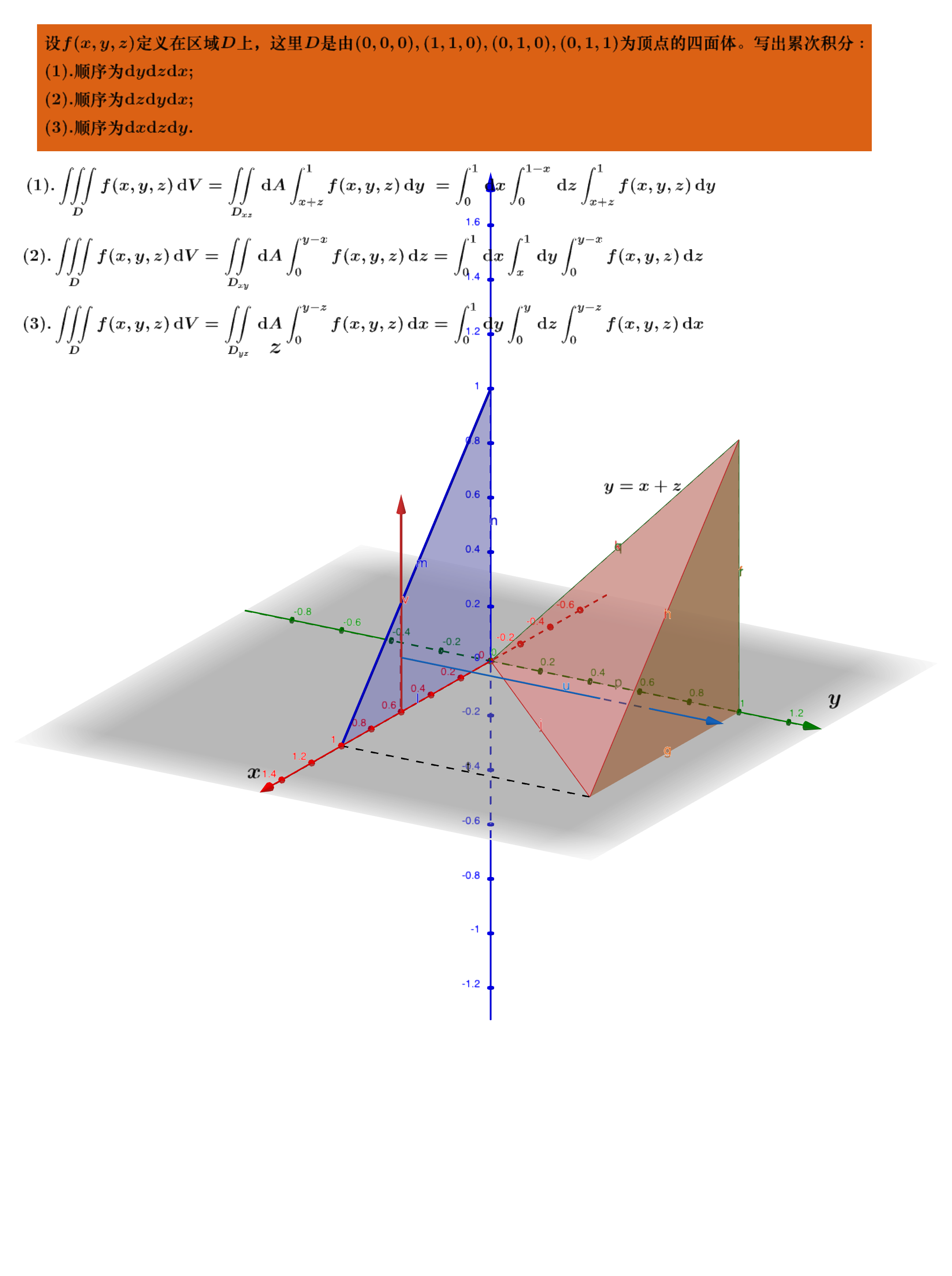
✏️例子
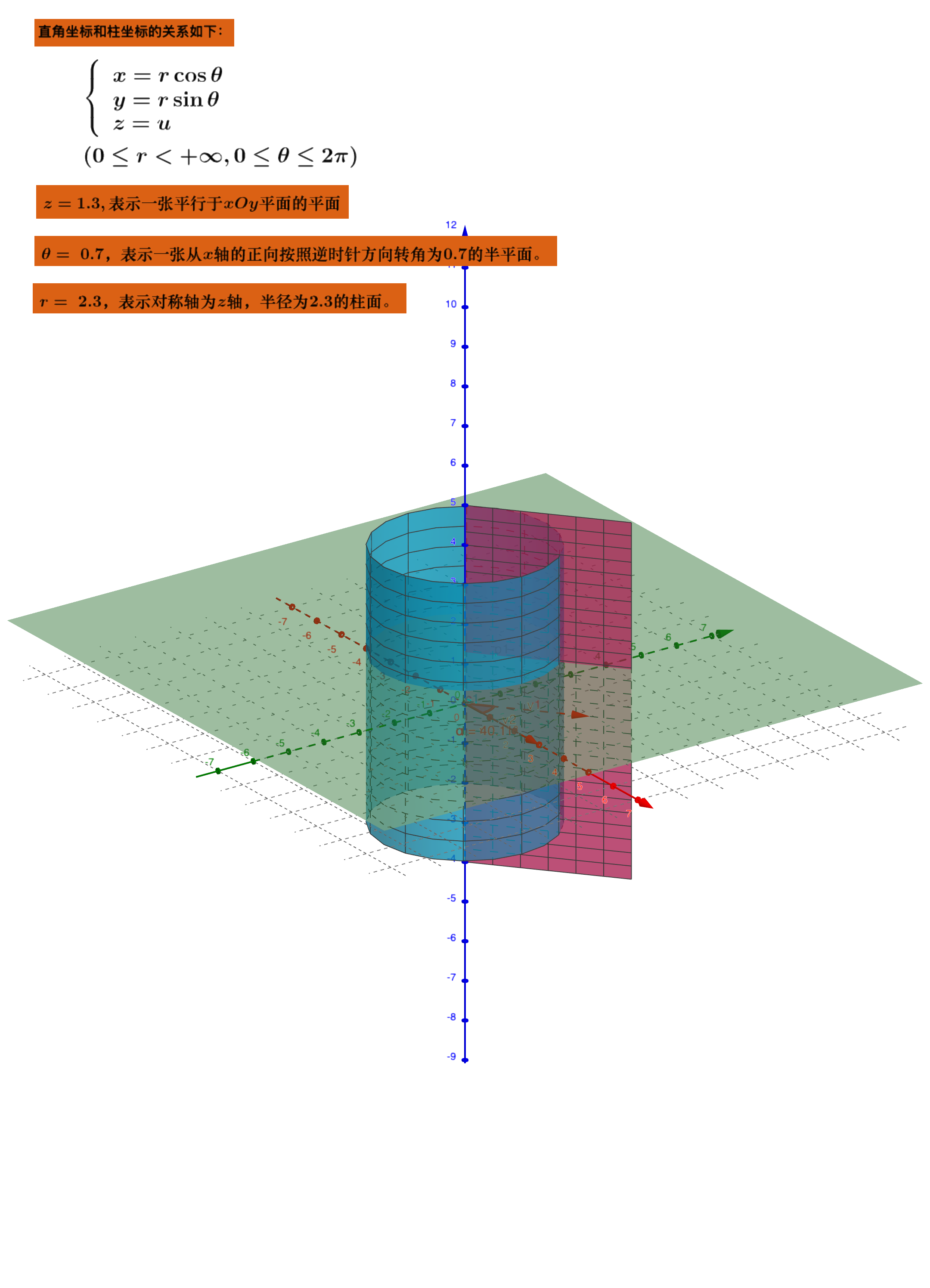
柱坐标下三重积分的计算
- 柱坐标:
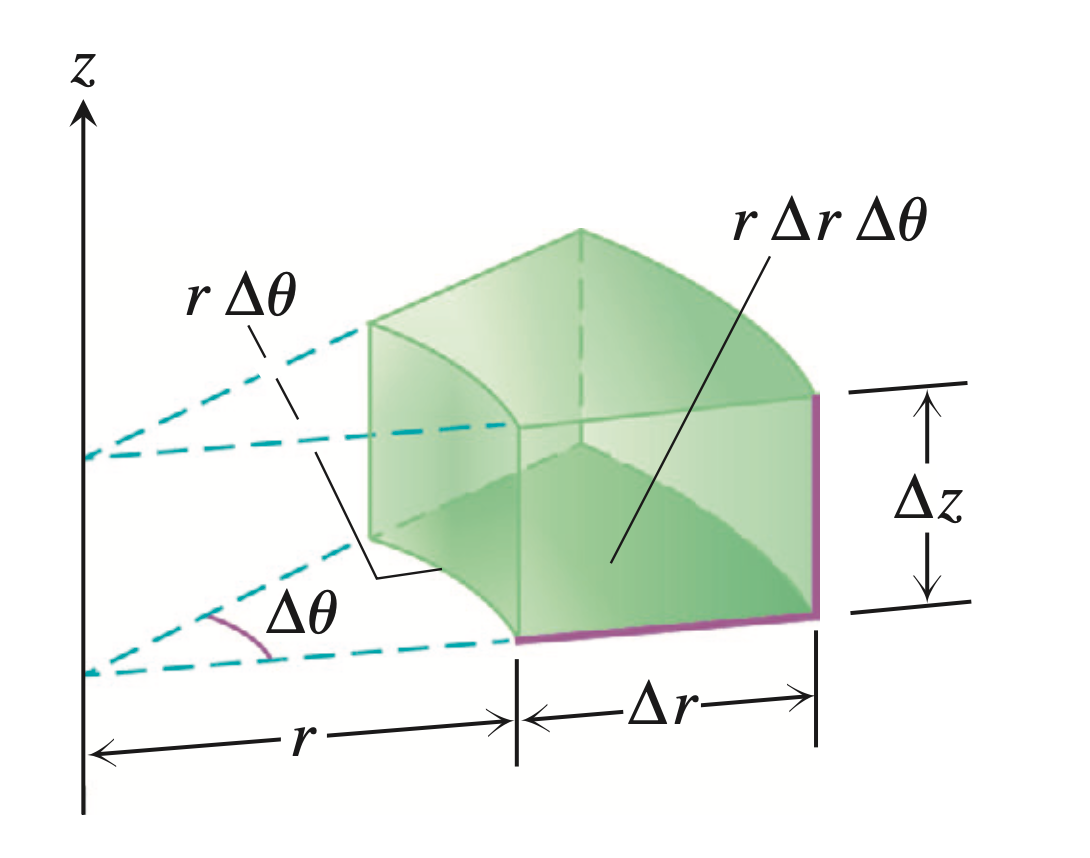
设$f(x,y,z)$定义在空间几何体$D$上,采用$r = r_1, r_2, \cdots, r_m, \theta = \theta_1, \theta_2, \cdots, \theta_n, z = z_1, z_2, \cdots, z_k$分割几何体$D$(该分割记为$P$)。这是体积元素为:
其计算见下图:
当分割的细度趋于零时,若极限存在,记为:
柱坐标下积分计算的步骤
画出空间区域$D$,并画出该几何体在坐标平面上的投影,写出边界曲面的方程。
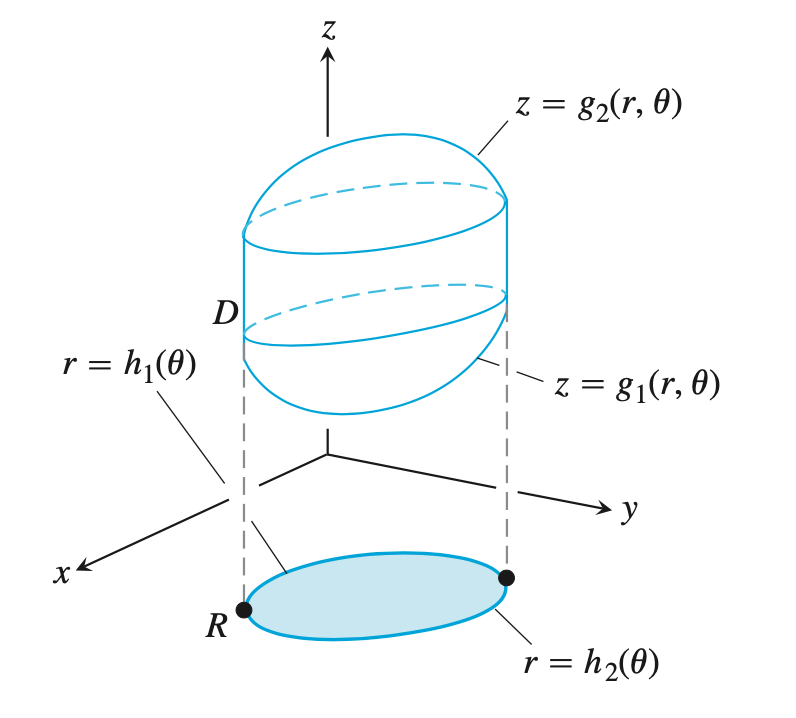
在投影区域上任取一点,作平行于$z$轴的平行线,找到射线的穿入边界(曲面)和穿出边界(曲面)。注意把边界曲面表达为极坐标的形式。
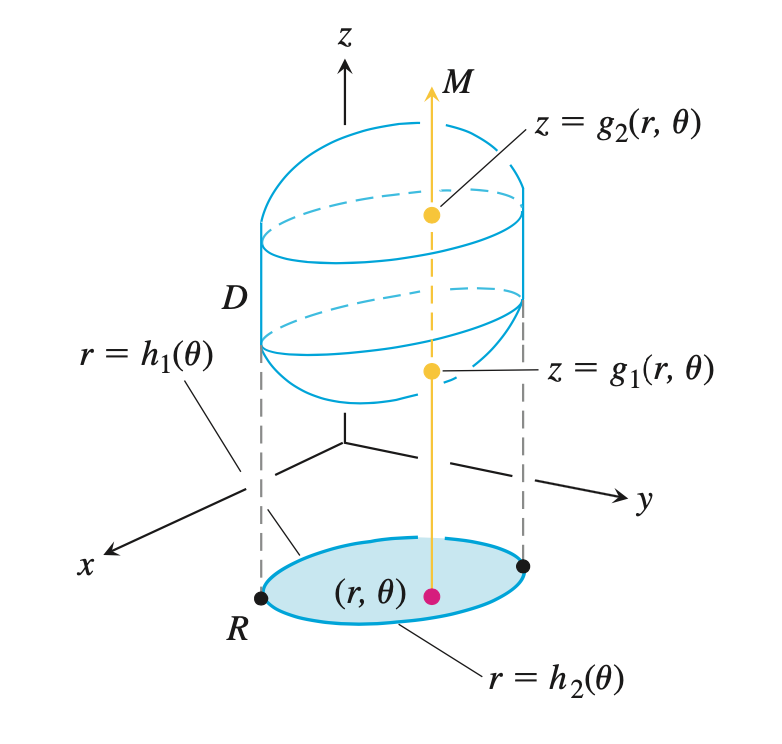
对投影区域,找到$r,\theta$的变化范围。在$xOy$平面上从原点出发画射线穿越投影区域,确定$r,\theta$的变换范围。
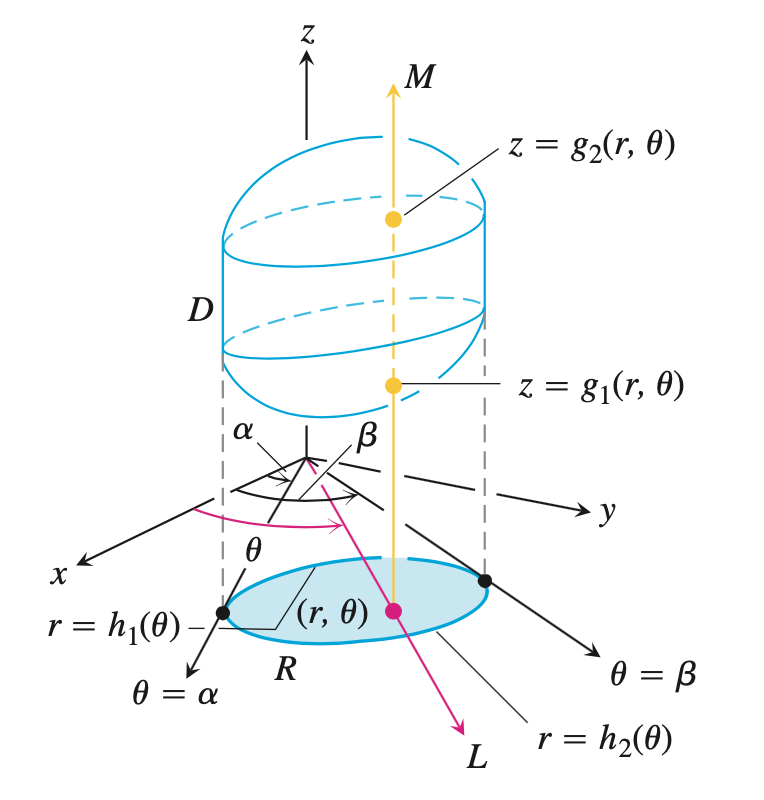
把重积分写为累次积分的形式,注意积分元素为:$\mathrm{d}zr\mathrm{d}r\mathrm{d}\theta$.
✏️例子
球坐标系

球坐标下的三重积分
设$f(x,y,z)$定义在空间几何体$D$上,采用$\rho = \rho_1,\rho_2,\cdots,\rho_m, \phi = \phi_1,\phi_2, \cdots, \phi_n, \theta = \theta_1, \theta_2, \cdots, \theta_k$分割几何体(分割记为$P$)。体积元素为:$\Delta V_k = \rho_k^2 \sin \phi_k \Delta \phi_k \Delta \rho_k \Delta \theta_k $
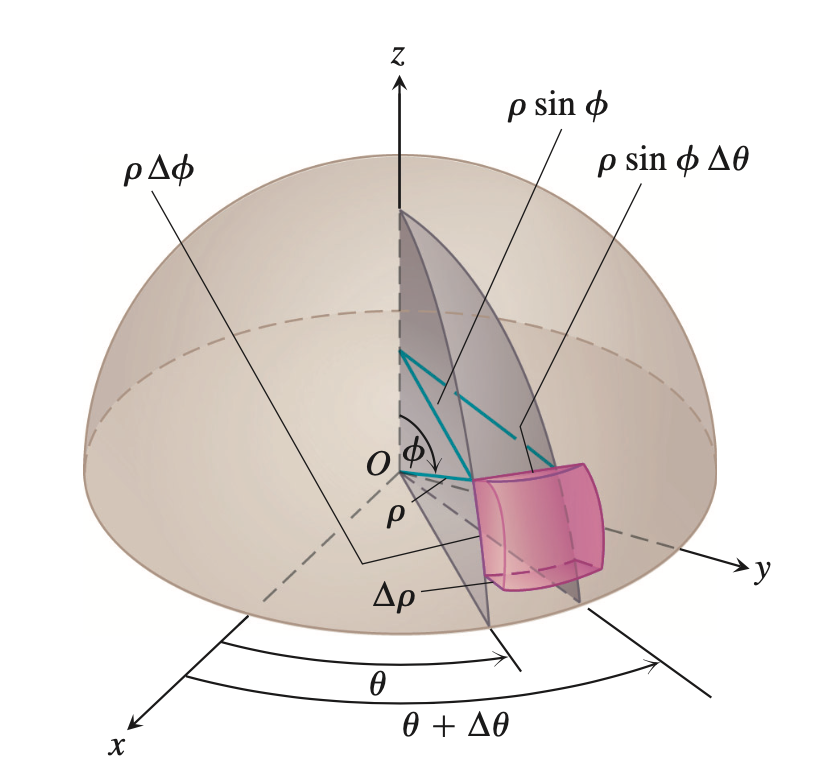
若当分割$P$的细度趋于零时,和式极限存在,记为:
球坐标系积分计算步骤
- 画出空间积分区域,写出几何体边界曲面的球坐标表达式,并画出在坐标平面上的投影;
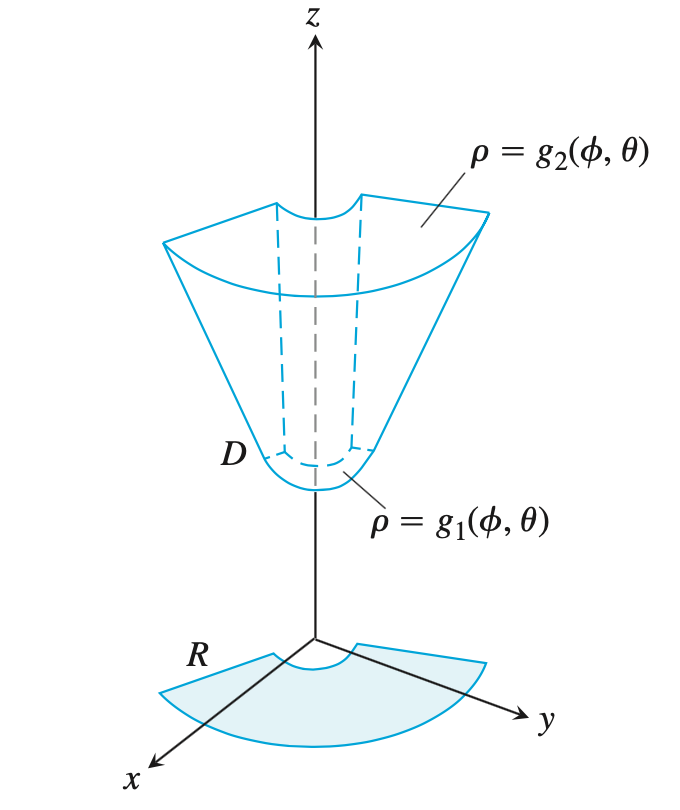
找出$\rho$的积分上下限。过原点作射线,该射线穿越积分几何体。找到射线的穿入边界(积分下限)和穿出边界(积分上限)。注意:几何体的边界曲面需要用球坐标表示;
找到$\phi$的变化范围:从$z$轴的正向开始,向$xOy$面倾斜。找到$\phi$的变化范围,即$\phi$的积分下限和上限;
找到$\theta$的变化范围:从$(0,0,0)$点出发,在$xOy$面上作射线穿越投影区域,找到$\theta$的变化范围,即$\theta$积分的下限和上限。
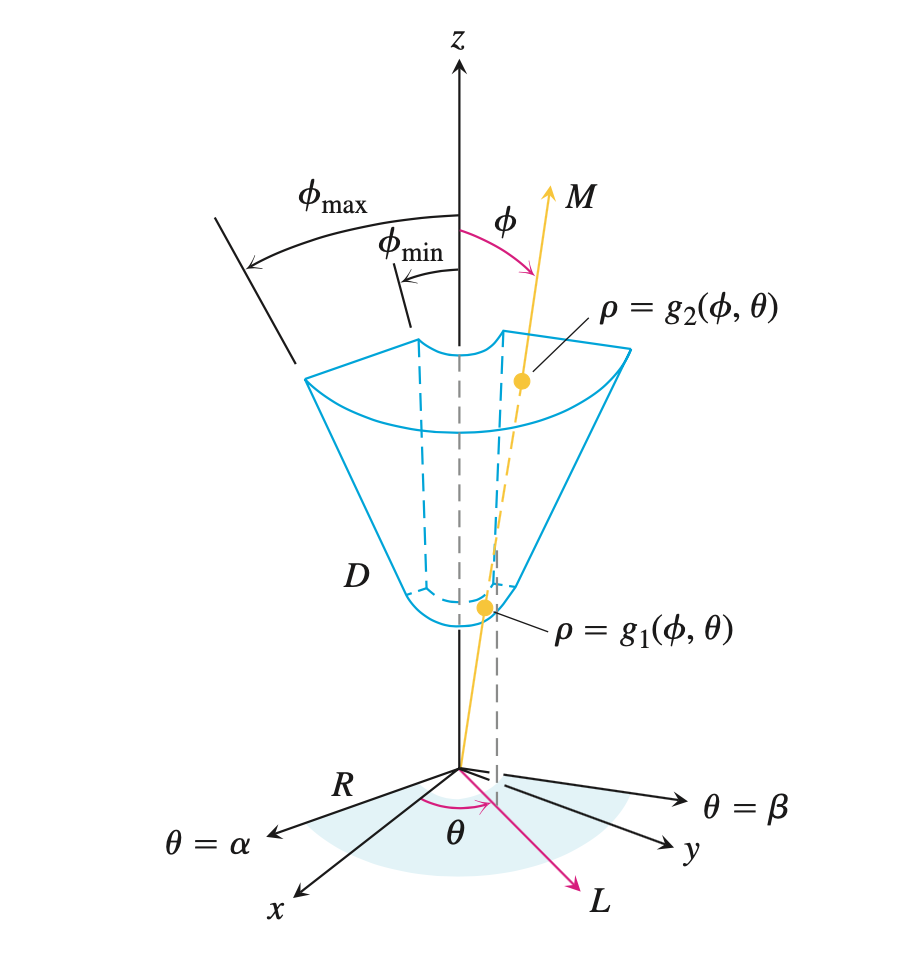
转换三重积分为球坐标系下的累次积分。
$$\iiint\limits_{D}f(x,y,z)\, \mathrm{d}V = \int_{\theta = \alpha}^{\theta = \beta} \mathrm{d}\theta \int_{\phi = \phi_{min}}^{\phi = \phi_{max}}\sin \phi\mathrm{d}\phi\int_{\rho = g_1(\phi, \theta)}^{i\rho=g_2(\phi,\theta)}\rho^2\mathrm{d}\rho $$
✏️例子
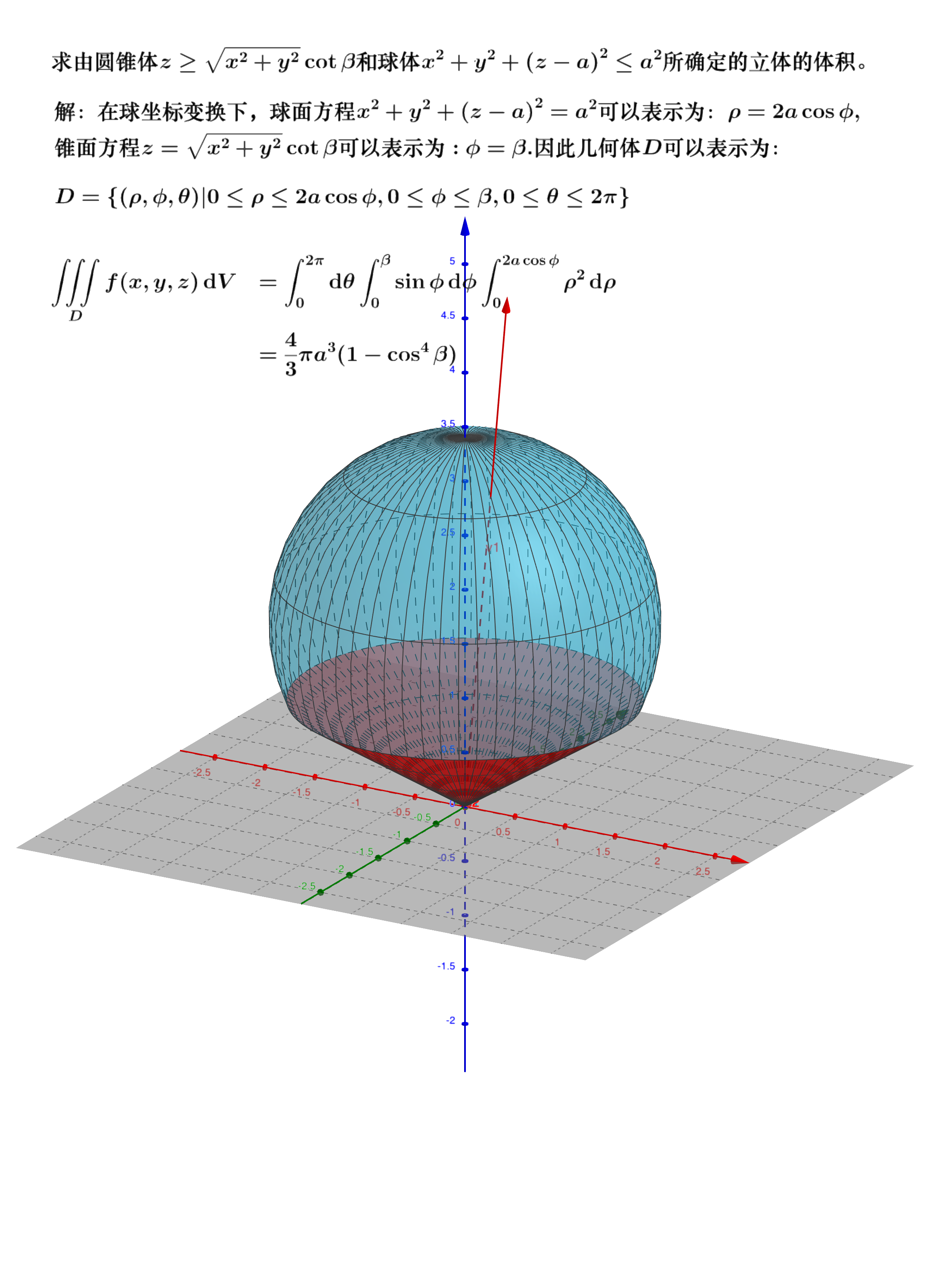
📚第三次作业:
计算下列积分:
$\iiint\limits_{V} (xy + z^2)\, \mathrm{d}v$,其中$V = [-2, 5] \times [-3, 3] \times [0,1]$;
$\iiint\limits_{V} x \cos y \cos z\, \mathrm{d}v$,其中$V = [0, 1] \times \left[0, \dfrac{\pi}{2}\right] \times \left[0, \dfrac{\pi}{2}\right]$;
$\iiint\limits_{V} (x + y + z)^2\, \mathrm{d}v$,其中$V$由曲面$z = \sqrt{2 - x^2 - y^2}$以及$z = x^2 + y^2$所围成的闭区域;
$\iiint\limits_{V} (x + y + z)^2\, \mathrm{d}v$,其中$V$由曲面$z = \sqrt{2 - x^2 - y^2}$以及$z = 0$所围成的闭区域;
📌4. 重积分的应用
曲面的表面积
设一空间曲面,其方程为$f(x,y,z)=c$,其在坐标平面上的投影为$R$,见下图。如何求解该曲面的面积?
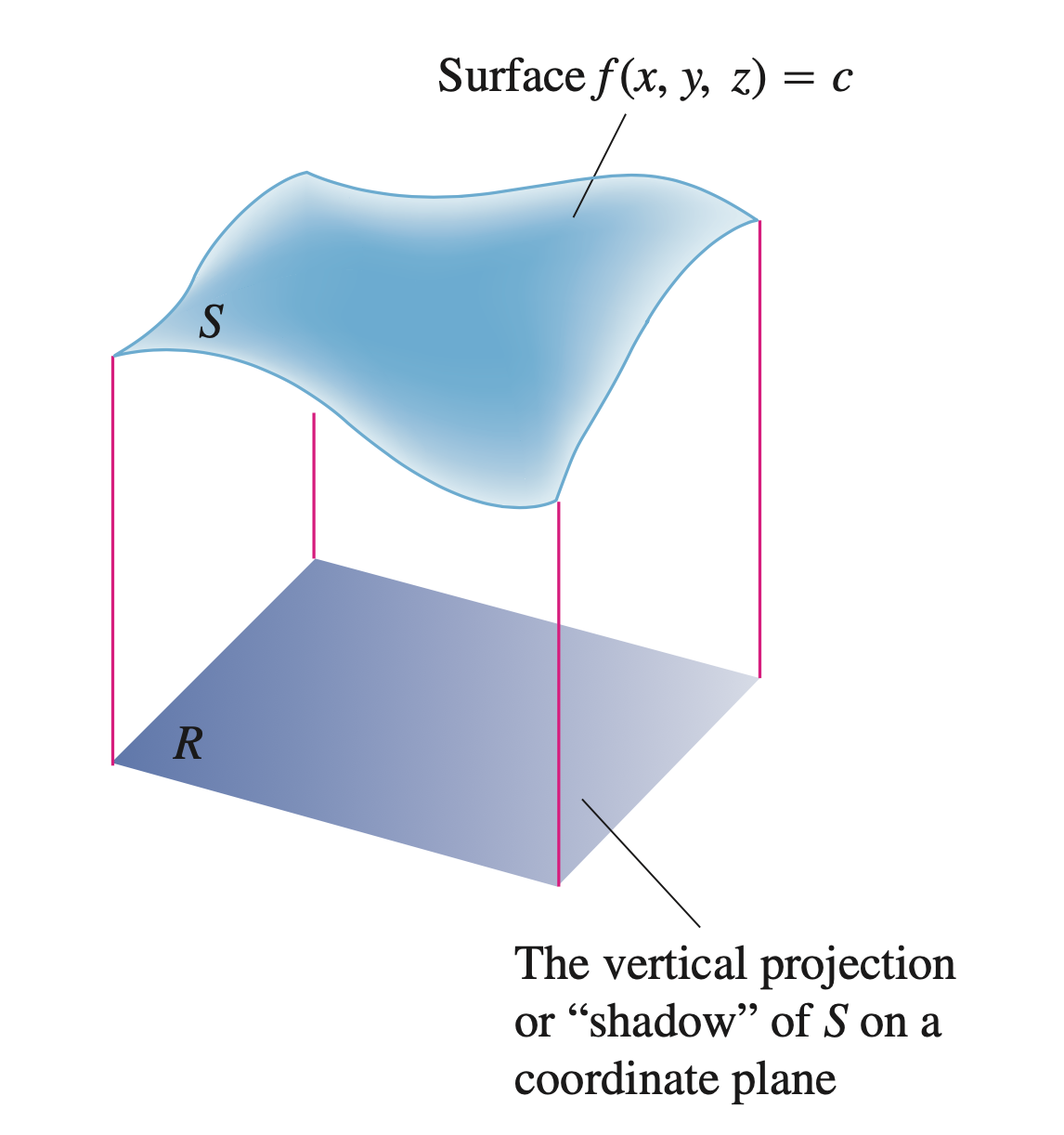
- 对区域$R$进行分割,在第$k$块小区域上向上作柱面截得曲面的面积为$\Delta \sigma_k$,截的曲面在$T_k(x_k,y_k,z_k)$处且平面的面积为$\Delta P_k$。则有
- $\mathbf{p}$在$T_k(x_k, y_k,z_k)$处垂直与投影平面$R$,$u_k, v_k$为且平面上截出部分两个边的向量。则有以下关系:
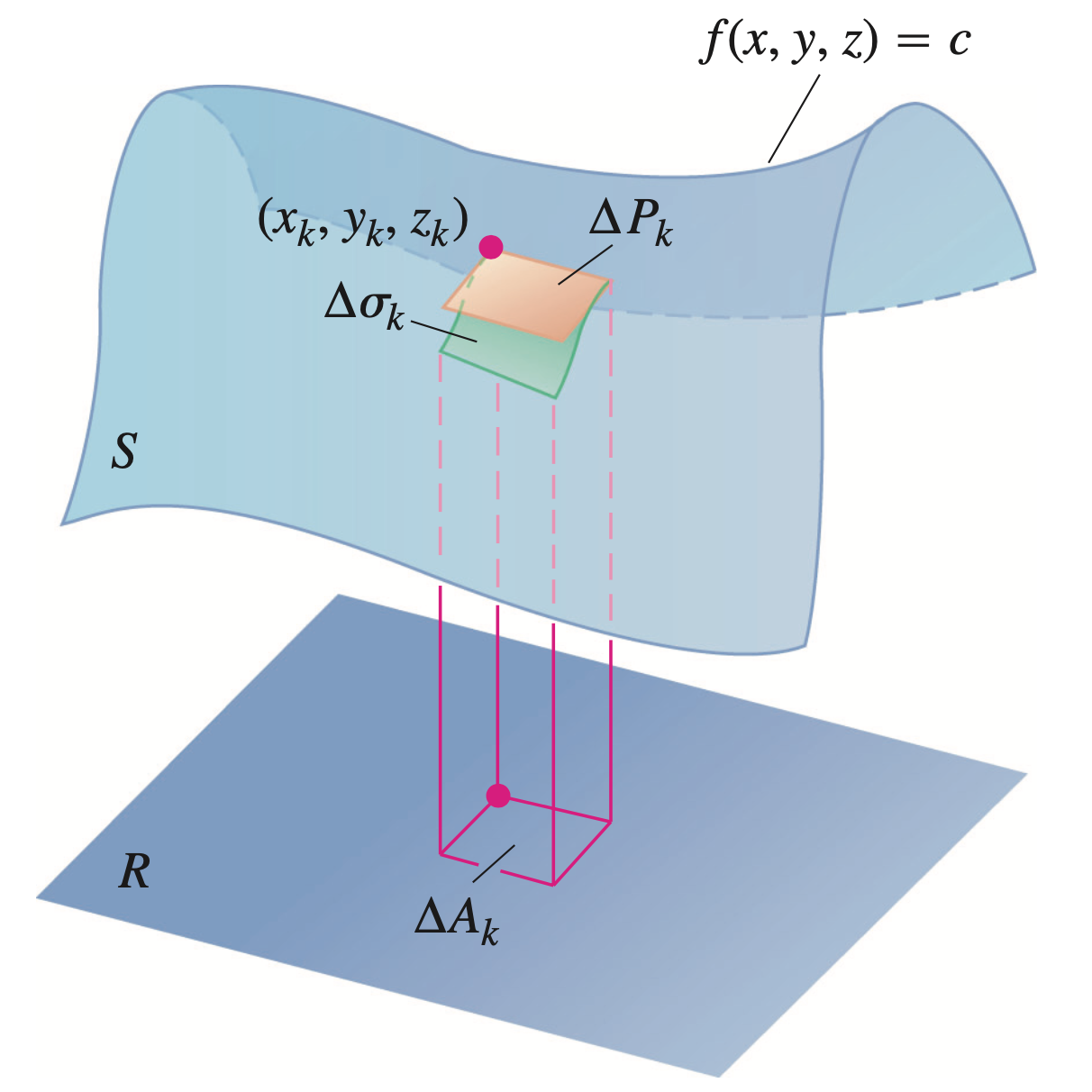
则有:
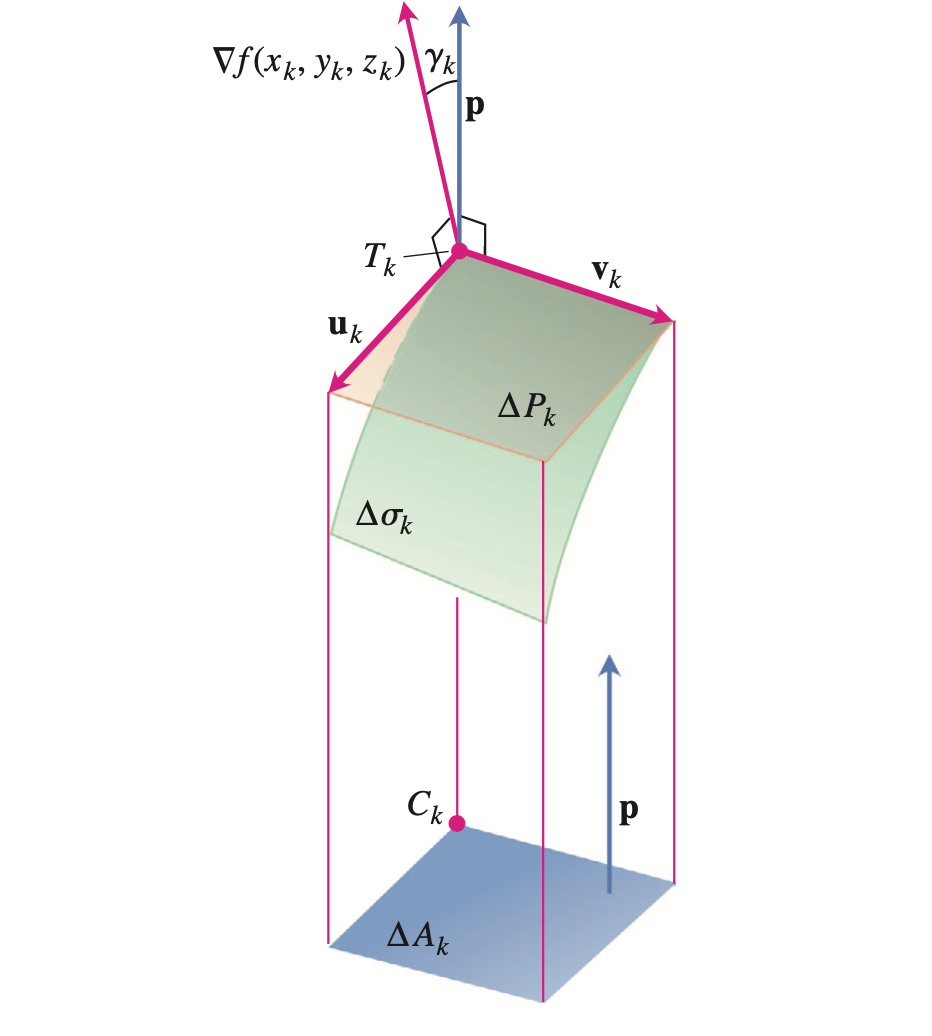
- 所以有曲面的面积为:
空间曲面如果可以表达为$z=f(x,y)$
若空间曲面的方程为$z = f(x,y),(x,y) \in R$,则
这时,曲面的面积表达式为:
\[S = \iint\limits_{R} \sqrt{1+f_x^2(x,y) + f_y^2(x,y)}\, \mathrm{d}A\]✏️例子
📚第四次作业:
求球面$x^2 + y^2 + z^2 = a^2$含在柱面$x^2 + y^2 = ax$内部的那部分面积。
求底圆半径相等的两个直交圆柱面$x^2 + y^2 = R^2$及$x^2 + z^2 = R^2$所围立体的表面积。
📚参考书目
📖1. 《高等数学》上下册(第七版),同济大学,高等教育出版社,2014.7.
📖2. 《数学分析》上下册(第二版),陈纪修、於崇华、金路,高等教育出版社,2004.
📖3. 《数学分析》上下册(第二版),华东师范大学数学系,高等教育出版社,2010.
📖4. Mathematical Analysis I,II, 2nd ed. V. A. Zorich, Springer, 2015.
📖5. 数学分析中的典型问题与方法, 裴礼文, 高等教育出版社, 2015.
📖6. Thomas’s Calculus, Weir, Maurice D etc., Addison-Wesley, 2010.
Calculus and its Visualization: an Introduction
👏 THANKS



