定积分的应用
Undergraduate course, China University of Petroleum at Beijing, Department of Science, 2020
这部分介绍一元函数定积分的应用。
目录
📌1. 求平面图形面积
直角坐标下求面积
一般地,求由$y = f_2(x), y = f_x(x)$以及两条直线$x = a, x = b$所围成的图形的面积为:
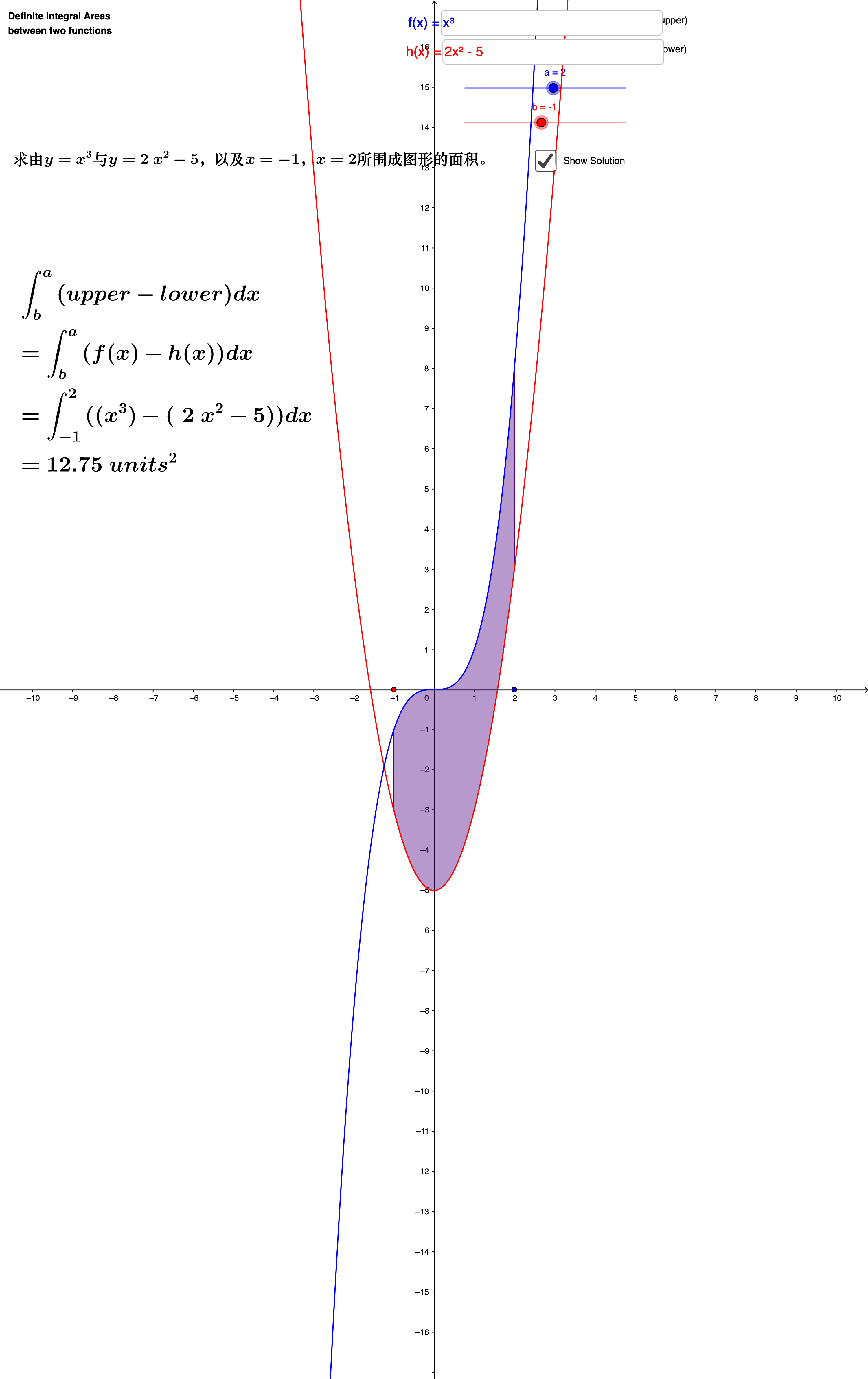
参数方程下求面积
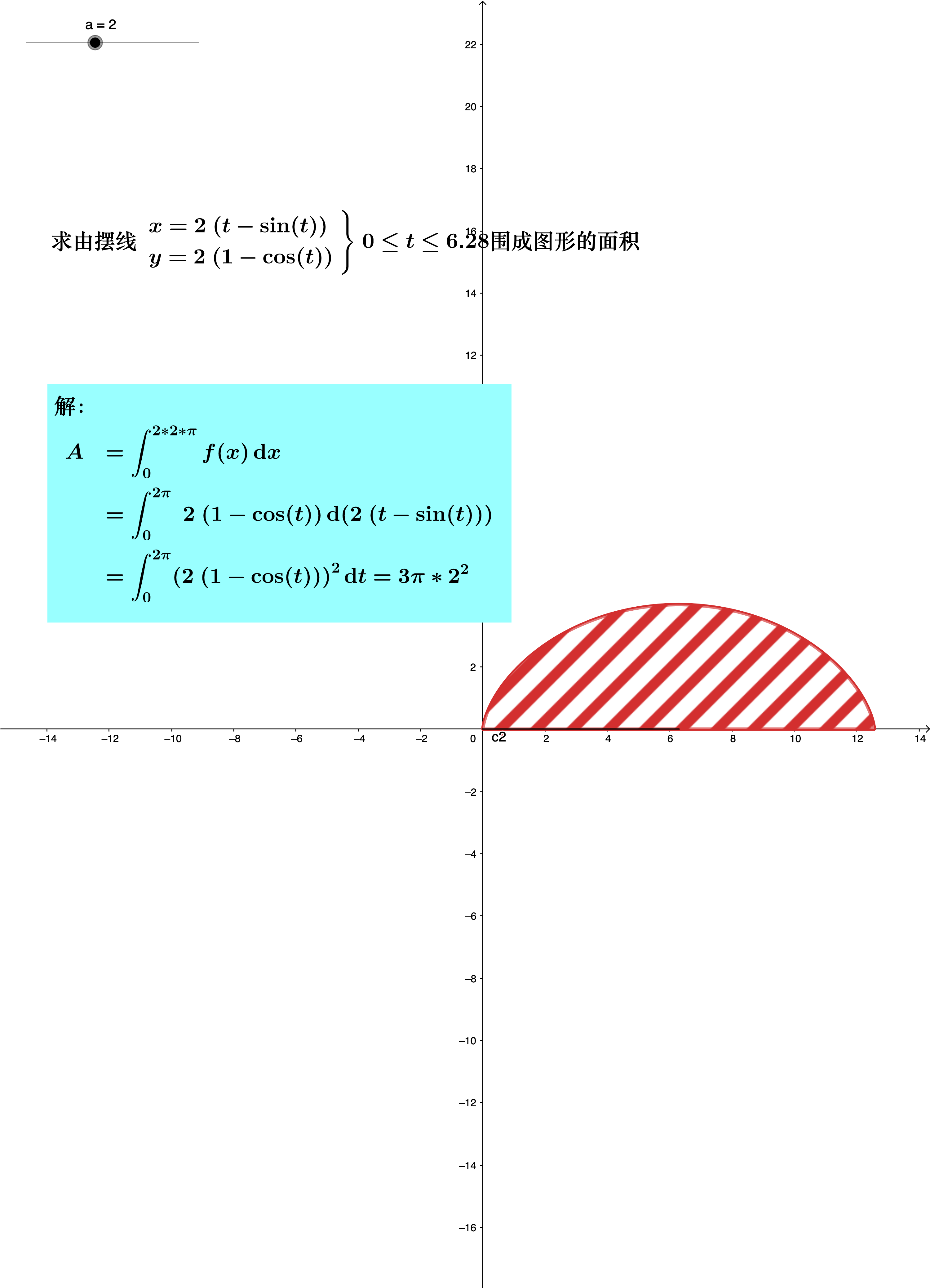
极坐标下求二重积
极坐标下求面积公式为:
下图为公式的推导,及其求$r = 4 + 4\cos \theta(0 \le \theta \le 2\pi)$的面积。
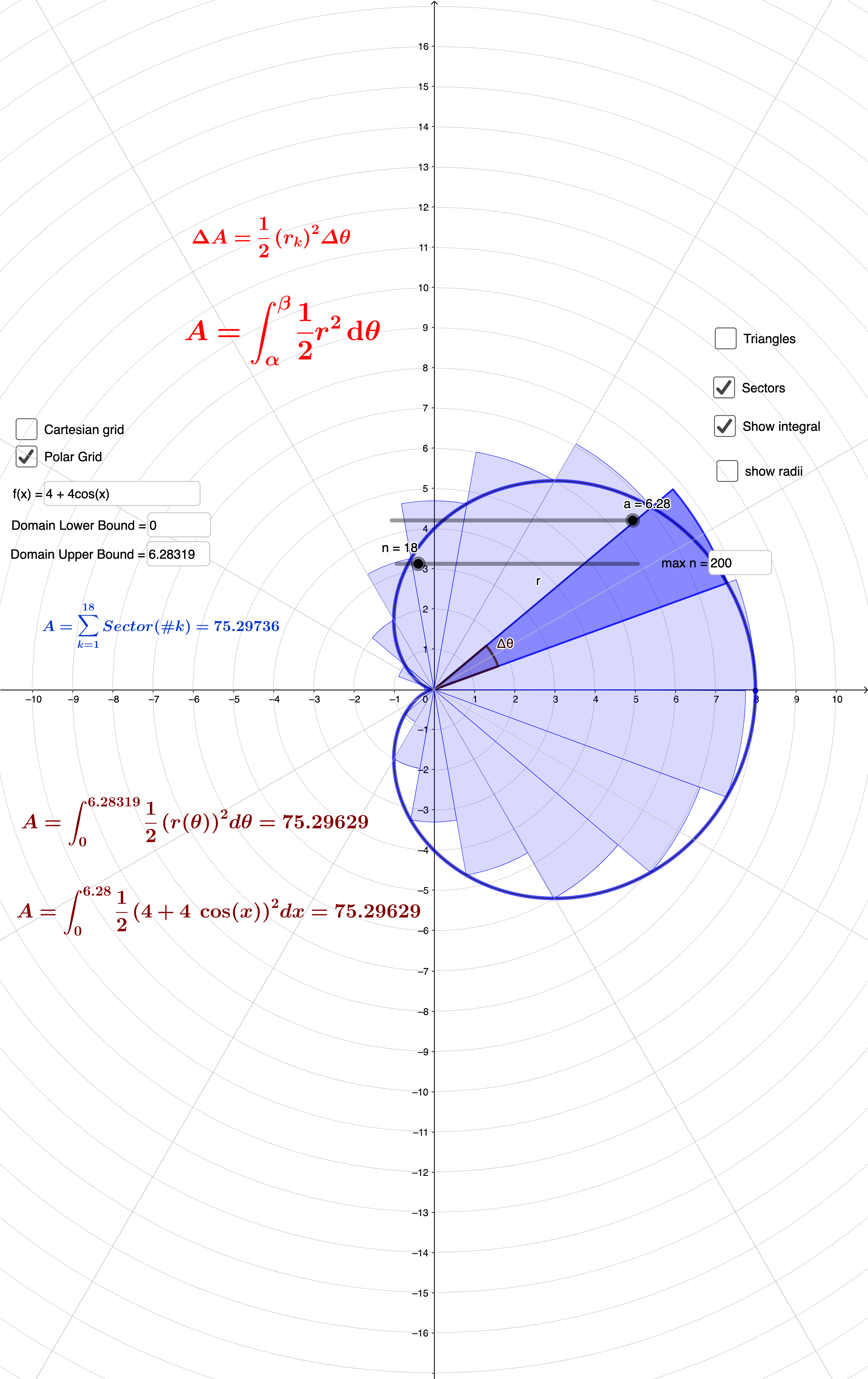
📌1. 求界面为已知的几何体的体积
设一个几何体$S$自变量$x$的变化范围为:$[a,b]$.在$x$处的截面的面积为$A(x)$,
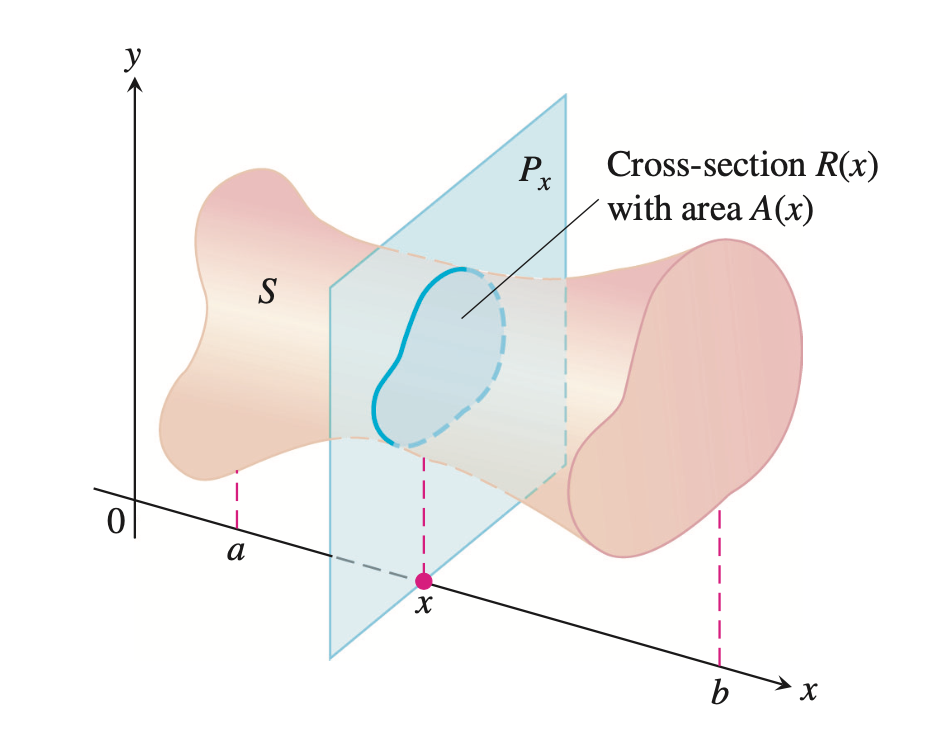
当区间$[a,b]$被分割为:
则在$[x_{k-1},x_k]$区间上对应的几何体体积约为:
其中$x_k = x_k - x_{k-1}, A_k$为$x = x_k$处的切面的面积。
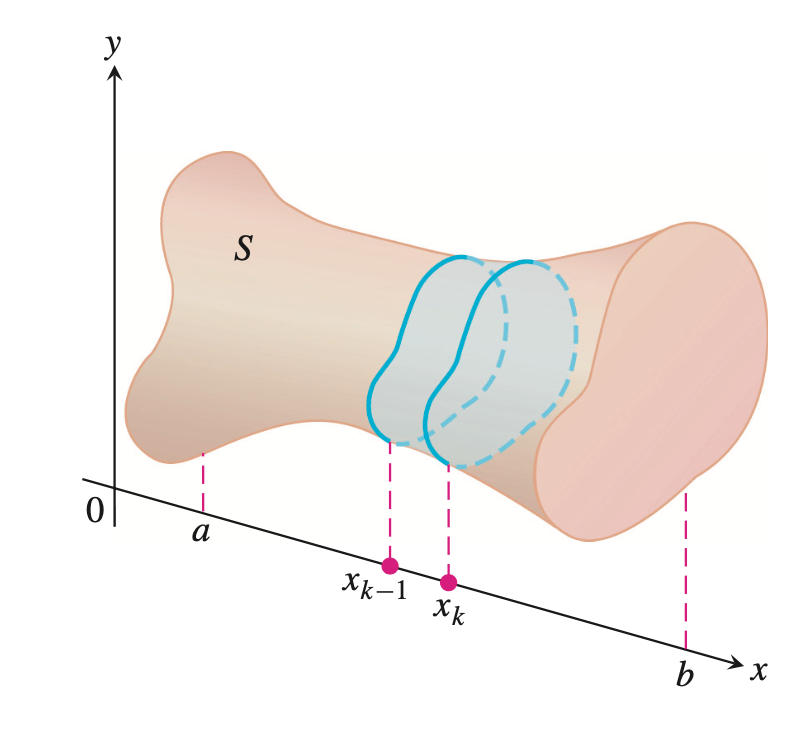
所以几何体$S$的体积为:
✏️例子
设一个锥体高度为3米,地面为3米的正方形,其垂直于$x$轴的截面的边长为$x$米,求其体积。
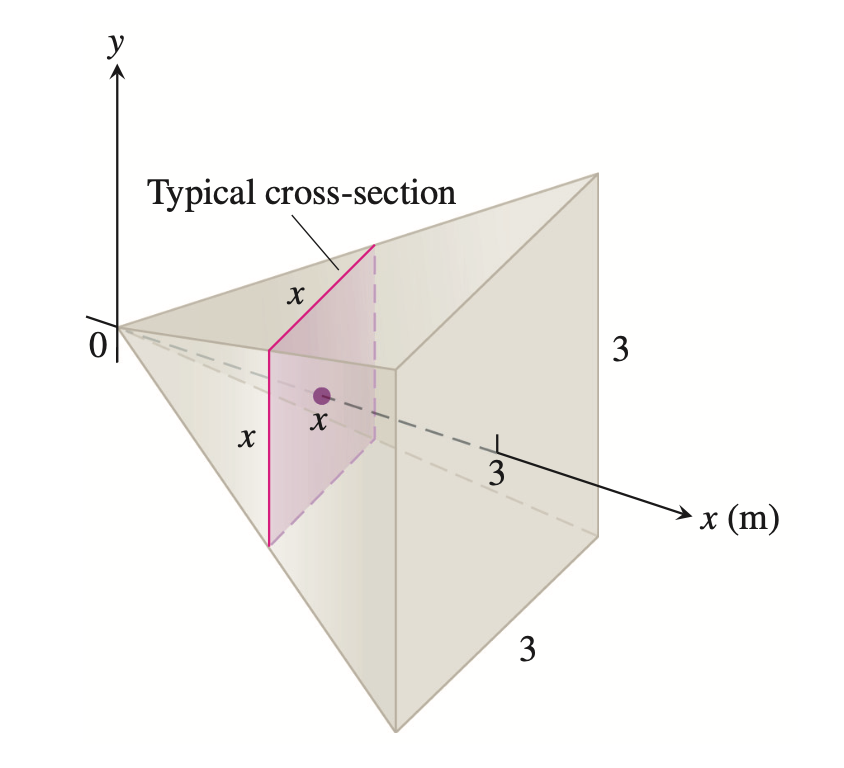
解: $V \int_0^3 x^2\,\mathrm{d}x = \left[\dfrac{x^3}{3}\right]_0^3 = 9m^3$
✏️例子
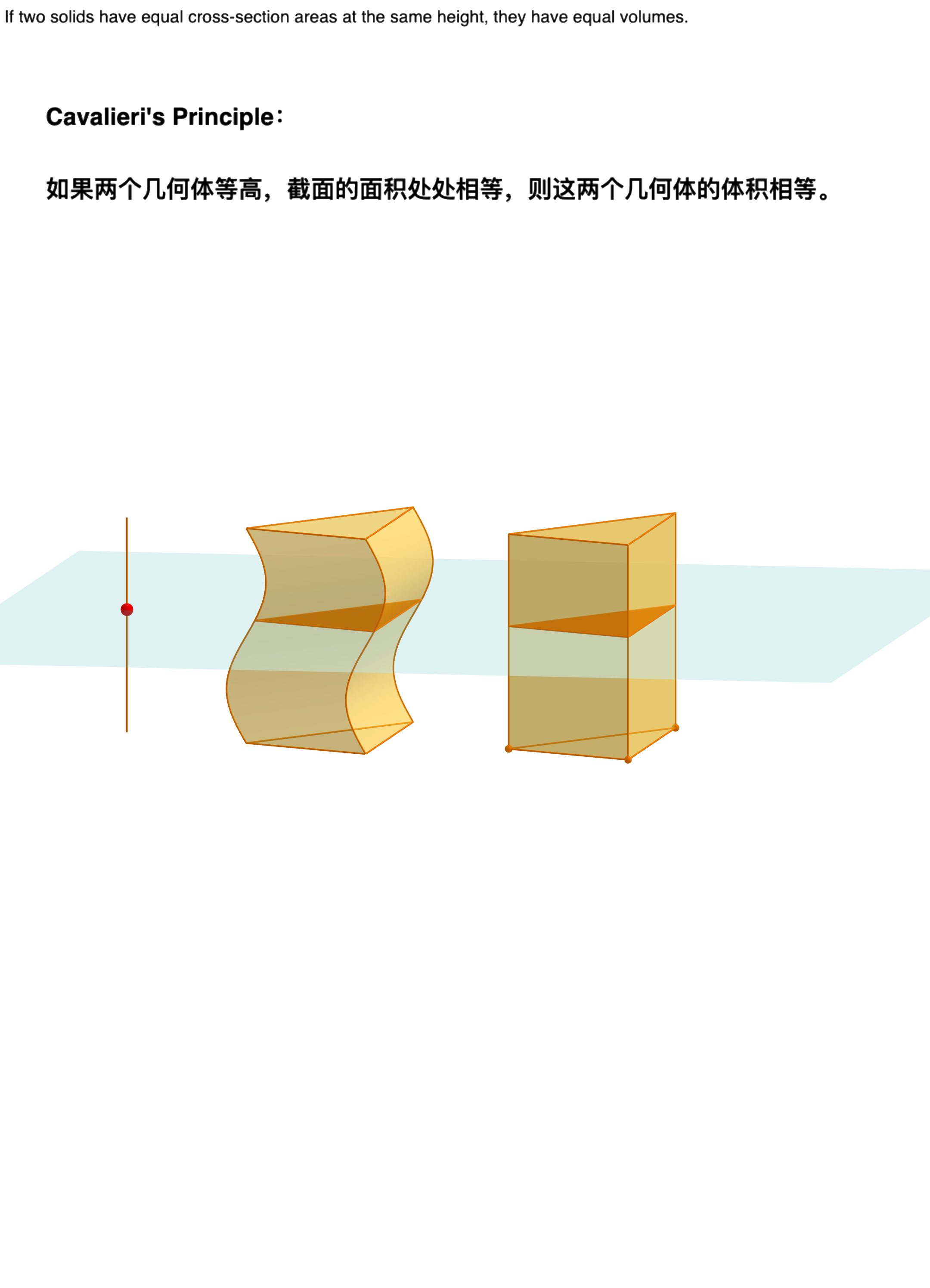
祖暅原理
✏️例子
求下列楔形几何体的体积
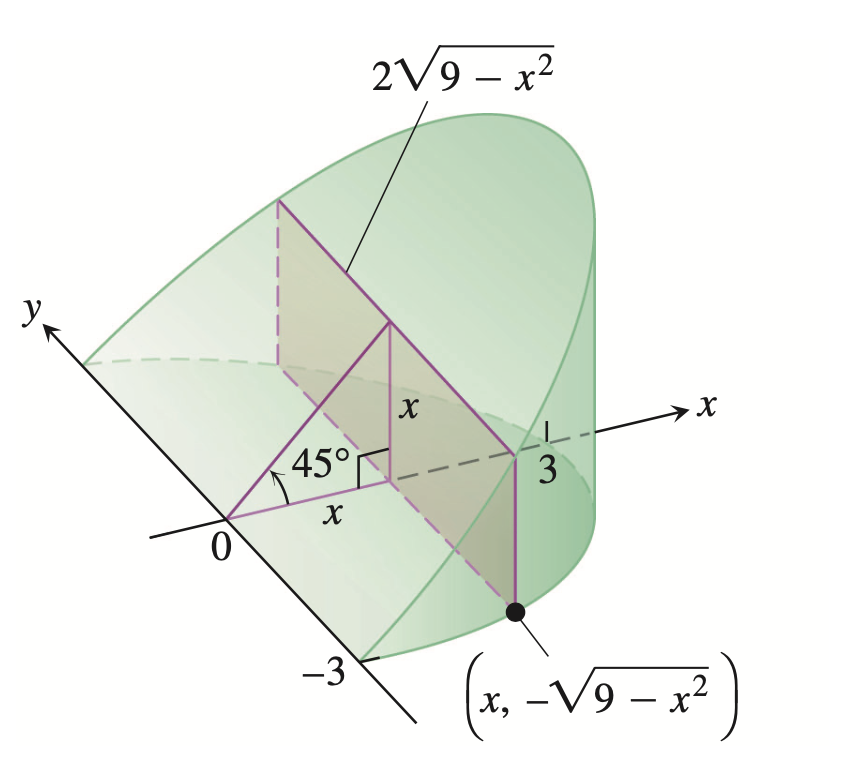
解: $V = \int_a^b A(x)\, \mathrm{d}x = \int_0^3 2x \sqrt{9 - x^2}\, \mathrm{d}x = 18$
📌3. 求平面曲线的弧长
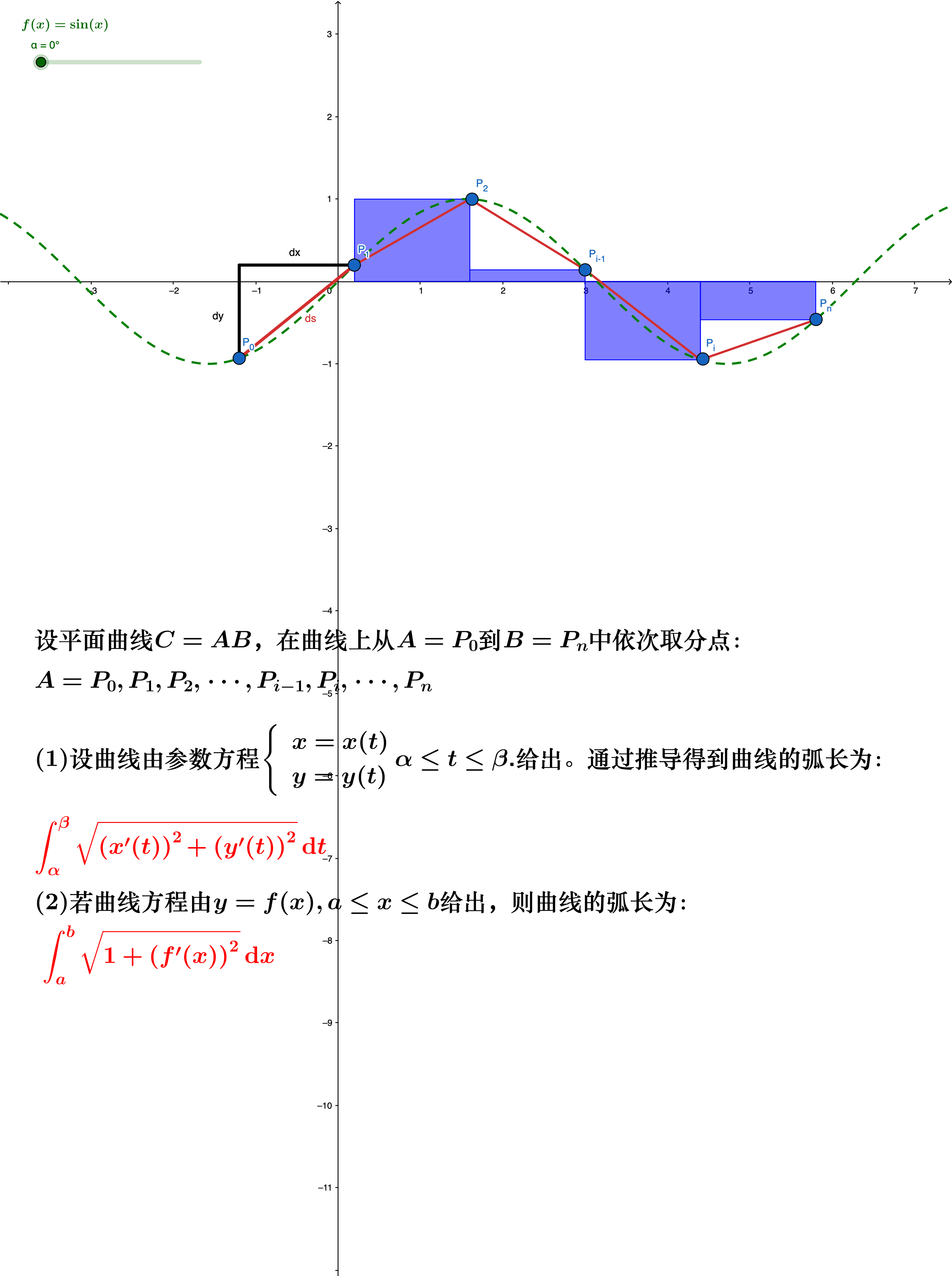
Calculus and its Visualization: an Introduction
👏 THANKS



